2023年重庆市高考数学质检试卷（5月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若2730能被不同的偶数整除，则这样的偶数个数有（　　）

  A．14

  B．15

  C．16

  D．17
  组卷：164引用：3难度：0.6

  解析

• 2．复数a+bi（a,b∈R）与复平面内的点（a,b）一一对应，则复平面内的点（2，3）对应的复数是（　　）

  A．2+3i

  B．1+i

  C．4-i

  D．5-i
  组卷：59引用：1难度：0.8

  解析

• 3．已知动直线l的方程为（1-a²）x+2ay-3a²-3=0，a∈R，

  P

  （

  3

  ，

  1

  ）

  ，O为坐标原点，过点O作直线l的垂线，垂足为Q，则线段PQ长度的取值范围为（　　）

  A．（0，5]

  B．[1，5]

  C．[5，+∞）

  D．（0，3]
  组卷：473引用：5难度：0.7

  解析

• 4．已知

  a

  lo

  g

  4

  a

  =

  16

  2

  ，则a+log₂a=（　　）

  A．11或 - 23 8

  B．11或 - 21 8

  C．12或 - 23 8

  D．10或 - 21 8
  组卷：554引用：5难度：0.7

  解析

• 5．已知正九边形A₁A₂⋯A₉，从

  A

  1

  A

  2

  ，

  A

  2

  A

  3

  ，…，

  A

  9

  A

  1

  中任取两个向量，则它们的数量积是正数的概率为（　　）

  A． 1 2

  B． 2 3

  C． 4 9

  D． 5 9
  组卷：87引用：3难度：0.7

  解析

• 6．已知正方体ABCD-A₁B₁C₁D₁的顶点都在表面积为12π的球面上，过球心O的平面截正方体所得的截面为一菱形，记该菱形截面为S，点P是正方体表面上一点，则以截面S为底面，以点P为顶点的四棱锥的体积的最大值为（　　）

  A． 8 3

  B． 7 3

  C．2

  D． 5 3
  组卷：82引用：2难度：0.4

  解析

• 7．被誉为“中国现代数学之父”的著名数学家华罗庚先生于1946年9月应普林斯顿大学邀请去美国讲学，之后又被美国伊利诺依大学聘为终身教授．新中国成立的消息使华罗庚兴奋不已，他放弃了在美国的优厚待遇，克服重重困难，终于回到祖国怀抱，投身到我国数学科学研究事业中去．这种赤子情怀，使许多年轻人受到感染、受到激励，其中他倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用，0.618就是黄金分割比

  t

  =

  5

  -

  1

  2

  的近似值，黄金分割比还可以表示成2sin18°，则

  t

  4

  -

  t

  2

  1

  -

  2

  co

  s

  2

  27

  °

  的值为（　　）

  A．-4

  B．4

  C．-2

  D．2
  组卷：198引用：5难度：0.8

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

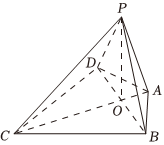• 21．如图，四棱锥P-ABCD的底面ABCD为筝形，AC∩BD于O点，O为AC的五等分点，

  AC

  =

  5

  6

  ，

  PA

  =

  30

  ，

  S

  底

  =

  30

  3

  ，且∠ADC=∠ABC=∠APC=90°．
  （1）求证：AC⊥PB；
  （2）作出平面PBA与平面PCD所成二面角α的任意一条棱，并求该二面角α的余弦值．
  组卷：98引用：3难度：0.5

  解析

• 22．已知函数f（x）=lnx-e^x+mx,其中m∈R，函数g（x）=f（x）+e^x+1．
  （Ⅰ）当m=1时，求函数f（x）在x=1处的切线方程；
  （Ⅱ）当m=-e时，
  （i）求函数g（x）的最大值；
  （ii）记函数φ（x）=|g（x）|-

  g

  （

  x

  ）

  +

  ex

  -

  1

  x

  -

  1

  2

  ，证明：函数φ（x）没有零点．
  组卷：113引用：5难度：0.3

  解析