2022-2023学年福建省福州市仓山区金港湾实验学校九年级（上）第一次适应性数学试卷

一、选择题（共10小题，每小题3分，满分30分）

• 1．下列各式中，y是x的二次函数的是（　　）

  A． y = 1 x 2

  B．y=2x+1

  C．y=x2+x-2

  D．y2=x2+3x
  组卷：2632引用：24难度：0.9

  解析

• 2．抛物线y=2x²+1的顶点坐标是（　　）

  A．（2，1）

  B．（0，1）

  C．（1，0）

  D．（1，2）
  组卷：1115引用：14难度：0.9

  解析

• 3．二次函数y=ax²+bx-1（a≠0）的图象经过点（1，1），则a+b+1的值是（　　）

  A．-3

  B．-1

  C．2

  D．3
  组卷：4651引用：82难度：0.9

  解析

• 4．抛物线y=x²-2x-3与x轴的交点个数是（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：1782引用：16难度：0.9

  解析

• 5．二次函数y=ax²+bx+c的部分对应值如表：
  

  x	…	-2	-1	0	1	2	3	…
  y	…	5	0	-3	-4	-3	0	…

  二次函数图象的对称轴是（　　）

  A．直线x=1

  B．y轴

  C．直线x= 1 2

  D．直线x=- 1 2
  组卷：136引用：6难度：0.9

  解析

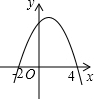• 6．如图，二次函数y=ax²+bx+c的图象与x轴交于（-2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（　　）

  A．x＜-2

  B．x＞4

  C．-2＜x＜4

  D．x＞0
  组卷：952引用：77难度：0.7

  解析

• 7．二次函数y=ax²+bx+c的图象如图所示，那么一次函数y=ax+b的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：7122引用：26难度：0.7

  解析

• 8．某种品牌的服装进价为每件150元，当售价为每件210元时，每天可卖出20件，现需降价处理，且经市场调查：每件服装每降价2元，每天可多卖出1件．在确保盈利的前提下，若设每件服装降价x元，每天售出服装的利润为y元，则y与x的函数关系式为（　　）

  A．y=- 1 2 x2+10x+1200（0＜x＜60）

  B．y=- 1 2 x2-10x+1250（0＜x＜60）

  C．y=- 1 2 x2+10x+1250（0＜x＜60）

  D．y=- 1 2 x2+10x+1250（x≤60）
  组卷：1989引用：9难度：0.9

  解析

三、解答题（共86分）

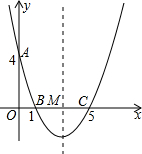• 24．如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．
  （1）求抛物线的解析式和对称轴；
  （2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
  （3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．
  组卷：24338引用：123难度：0.1

  解析

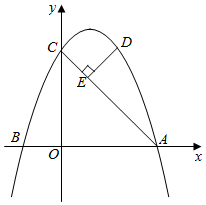• 25．直线AC：y=-x+3与x轴y轴的交点分别为A、C，B点坐标为（-1，0）．
  （1）若二次函数y=ax²+bx+c的图象恰好过A、C、B三点，求二次函数的解析式；
  （2）P为抛物线上一点，且∠PCO=∠POC，求点P的坐标；
  （3）该二次函数图象上有一点D（x,y）（其中x＞0，y＞0）．①做DE⊥AC，垂足为点E，若DE=CE，求D点坐标；
  ②线段DE是否存在最大值，若存在，求出D点坐标及这个最大值；若不存在，说明理由．
  组卷：422引用：2难度：0.3

  解析