2022-2023学年湖北省黄冈市部分高中高二（下）期中数学试卷

一、单项选择题（共8题，每题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知质点M在平面上做变速直线运动，且位移S（单位：m）与时间t（单位：s）之间的关系可用函数：S=ln（t+1）+2t²+1表示，则该质点M在t=2s时的瞬时速度为（　　）

  A． 25 3 m / s

  B．9+ln3m/s

  C． 25 6 m / s

  D．4+2ln3m/s
  组卷：25引用：1难度：0.9

  解析

• 2．林老师希望从{A，B，C}中选2个不同的字母，从{1，3，5，7}中选3个不同的数字编拟车牌号鄂J×××××的后五位，要求数字互不相邻，那么满足要求的车牌号有（　　）

  A．576个

  B．288个

  C．144个

  D．72个
  组卷：18引用：1难度：0.7

  解析

• 3．若函数f（x）=x²-4x+mlnx在区间[1，2]上是单调递增函数，则实数m的取值范围是（　　）

  A．（-∞，0]	B．[0，2]
  C．[2，+∞）	D．（-∞，0]∪[2，+∞）
  组卷：38引用：1难度：0.6

  解析

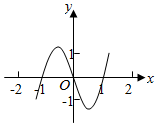• 4．已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），下面四个图象中，y=f（x）的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：913引用：54难度：0.9

  解析

• 5．若（x²+x+2y）⁵的展开式中x⁴y²的系数为M，

  （

  3

  x

  -

  x

  ）

  7

  展开式中各项系数和为N，则M、N大小关系为（　　）

  A．M＞N

  B．M＜N

  C．M=N

  D．无法确定
  组卷：100引用：1难度：0.5

  解析

• 6．已知函数f（x）=e^x+ax,若直线y=0为曲线y=f（x）的切线，则实数a的值为（　　）

  A．e

  B．-e

  C．0

  D．-1
  组卷：17引用：1难度：0.6

  解析

• 7．定义：两个正整数a,b,若它们除以正整数m所得的余数相等，则称a,b对于模m同余，记作a≡b（bmodm），比如：35≡25（bmod10）．
  已知：

  n

  =

  C

  0

  10

  -

  C

  1

  10

  10

  +

  C

  2

  10

  1

  0

  2

  -

  C

  3

  10

  1

  0

  3

  +

  ⋯

  +

  C

  10

  10

  1

  0

  10

  ，满足n≡p（bmod7），则p可以是（　　）

  A．26

  B．31

  C．32

  D．37
  组卷：86引用：3难度：0.5

  解析

四、解答题（共6题，共70分．解答应写出文字说明、证明过程或演算步骤）

• 21．为了积极响应国家“全面实施乡村振兴战略”的号召，某同学大学毕业后决定利用所学专业知识进行自主创业．经过市场调查，生产某种小型电子产品需投入固定成本3万元，每生产x万件，需另投入流动成本C（x）万元，当年产量小于10万件时，

  C

  （

  x

  ）

  =

  9

  x

  +

  7

  x

  -

  14

  （万元）；当年产量不小于10万件时，

  C

  （

  x

  ）

  =

  6

  x

  +

  lnx

  +

  4

  e

  x

  -

  13

  （万元）．已知每件产品售价为6元，假若该产品当年全部售完．
  （1）写出年利润P（x）（万元）关于年产量x（万件）的函数解析式；（注：年利润=年销售收入-固定成本-流动成本）
  （2）当年产量约为多少万件时，该产品所获年利润最大？最大年利润是多少？（结果保留一位小数，取ln2=0.7）
  组卷：30引用：5难度：0.6

  解析

• 22．已知函数f（x）=lnx-ax+1（a∈R）．
  （1）讨论f（x）的单调性；
  （2）若关于x的方程（a+x）lnx-ax²-xf（x）=0有两个相异的实数根x₁，x₂．求证：

  x

  1

  x

  2

  ＞

  e

  ．
  组卷：75引用：2难度：0.3

  解析