2023年山东省菏泽市成武县育青中学中考数学三模试卷

一、选择题（本大题共8个小题，每小题3分，共24分，在每小题给出的四个选项中，只有一个选项是正确的，请把正确选项的序号涂在答题卡的相应位置.）

• 1．下列各数中，负数是（　　）

  A．-1

  B．0

  C．2

  D．2023
  组卷：439引用：2难度：0.9

  解析

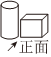• 2．如图，水平的讲台上放置的圆柱形笔筒和长方体形粉笔盒，其俯视图是（　　）

  A．

  B．

  C．

  D．
  组卷：125引用：6难度：0.7

  解析

• 3．对于实数a和b,定义一种新运算“⊗”为：a⊗b=

  1

  a

  -

  b

  2

  ，这里等式右边是实数运算．例如：1⊗3=

  1

  1

  -

  3

  2

  =

  -

  1

  8

  ．则方程x⊗2=

  2

  x

  -

  4

  -

  1

  的解是（　　）

  A．x=4

  B．x=5

  C．x=6

  D．x=7
  组卷：601引用：14难度：0.7

  解析

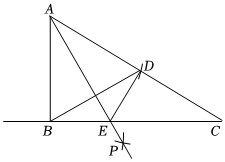• 4．如图，在△ABC中，∠ABC=90°，以点A为圆心，以AB的长为半径作弧交AC于点D，连接BD，再分别以点B，D为圆心，大于

  1

  2

  BD的长为半径作弧，两弧交于点P，作射线AP交BC于点E，连接DE，则下列结论正确的是（　　）

  A．DE垂直平分AC	B．△ABE∽△CBA
  C．BD2=BC•BE	D．CE•AB=DE•CA
  组卷：401引用：4难度：0.6

  解析

• 5．若一组数据1，2，4，3，x,0的平均数是2，则众数是（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：713引用：7难度：0.7

  解析

• 6．平面直角坐标系中，点P的坐标为（m,n），则向量

  OP

  可以用点P的坐标表示为

  OP

  =（m,n）；已知

  O

  A

  1

  =（x₁，y₁），

  O

  A

  2

  =（x₂，y₂），若x₁x₂+y₁y₂=0，则

  O

  A

  1

  与

  O

  A

  2

  互相垂直．
  下面四组向量：①

  O

  B

  1

  =（3，-9），

  O

  B

  2

  =（1，-

  1

  3

  ）；
  ②

  O

  C

  1

  =（2，π⁰），

  O

  C

  2

  =（2^-1，-1）；
  ③

  O

  D

  1

  =（cos30°，tan45°），

  O

  D

  2

  =（sin30°，tan45°）；
  ④

  O

  E

  1

  =（

  5

  +2，

  2

  ），

  O

  E

  2

  =（

  5

  -2，

  2

  2

  ）．
  其中互相垂直的组有（　　）

  A．1组

  B．2组

  C．3组

  D．4组
  组卷：255引用：2难度：0.7

  解析

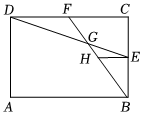• 7．如图，在矩形ABCD中，AB=6，AD=4，点E、F分别为BC、CD的中点，BF、DE相交于点G，过点E作EH∥CD，交BF于点H，则线段GH的长度是（　　）

  A． 5 6

  B．1

  C． 5 4

  D． 5 3
  组卷：5560引用：28难度：0.5

  解析

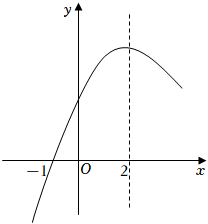• 8．二次函数y=ax²+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2，下列结论：（1）abc＜0；（2）4a+c＞2b；（3）3b-2c＞0；（4）若点A（-2，y₁）、点B（-

  1

  2

  ，y₂）、点C（

  7

  2

  ，y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）4a+2b≥m（am+b）（m为常数）．其中正确的结论有（　　）

  A．5个

  B．4个

  C．3个

  D．2个
  组卷：2173引用：10难度：0.5

  解析

三、解答题（本题共78分，把解答或证明过程写在答题卡的相应区域内）

• 23．如图，△AOB与△COD是等腰直角三角形，点O为直角顶点，连接AD、BC，E是BC的中点，连接OE
  
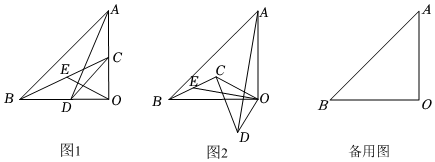
  （1）问题解决：如图①，当点C、D分别在OA、OB上时，线段EO与线段AD之间的数量关系为

  ；
  （2）类比探究：将△COD绕点O逆时针旋转到如图②所示位置，请探究线段EO与线段AD之间的数量关系，并说明理由；
  （3）拓展延伸：在△COD的旋转过程中，当△COD绕点O逆时针旋转时，若OA=8，OC=4，∠AOC=150°，请直接写出OE的长．
  组卷：259引用：5难度：0.2

  解析

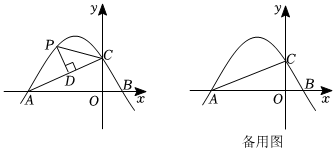• 24．如图，已知抛物线

  y

  =

  a

  x

  2

  -

  3

  2

  x

  +

  c

  与x轴交于点A（-4，0），B（1，0），与y轴交于点C．
  （1）求抛物线的解析式；
  （2）在抛物线的对称轴上是否存在点Q使QB+QC最小？若存在，请求出Q点坐标；若不存在，请说明理由；
  （3）点P为AC上方抛物线上的动点，过点P作PD⊥AC，垂足为点D，连接PC，当△PCD与△ACO相似时，求点P的坐标．
  组卷：573引用：5难度：0.3

  解析