2023-2024学年浙江省杭州十四中康桥校区高二（上）段考数学试卷（10月份）

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

• 1．在平面直角坐标系中，直线l：x+

  3

  y+1=0的倾斜角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：230引用：8难度：0.7

  解析

• 2．已知直线l的一个方向向量

  m

  =（2，-1，3），且直线l过A（0，y,3）和B（-1，2，z）两点，则y-z=（　　）

  A．0

  B．1

  C． 3 2

  D．3
  组卷：427引用：8难度：0.9

  解析

• 3．我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征．我们从这个商标中抽象出一个图象如图，其对应的函数可能是（　　）

  A． f （ x ） = 1 | x - 1 |

  B． f （ x ） = 1 | | x | - 1 |

  C． f （ x ） = 1 x 2 - 1

  D． f （ x ） = 1 x 2 + 1
  组卷：770引用：55难度：0.8

  解析

• 4．直线x+2ay-1=0与（a-1）x+ay+1=0平行，则a等于（　　）

  A． 3 2

  B． 3 2 或0

  C．0

  D．-2或0
  组卷：55引用：7难度：0.9

  解析

• 5．已知点A（

  3

  ，2），B（4，-3），若直线l过点P（0，1）与线段AB相交，则直线l的倾斜角的取值范围是（　　）

  A． [ π 3 ， 5 π 6 ]	B．[ π 6 ， 2 π 3 ]
  C． [ 0 ， π 6 ] ∪ [ 3 π 4 ， π ）	D． [ 0 ， π 3 ] ∪ [ 5 π 6 ， π ）
  组卷：1104引用：5难度：0.8

  解析

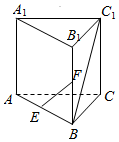• 6．如图所示，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AB=BC=AA₁，∠ABC=90°，点E、F分别是棱AB、BB₁的中点，则直线EF和BC₁所成的角是（　　）

  A．45°

  B．60°

  C．90°

  D．120°
  组卷：280引用：23难度：0.9

  解析

• 7．已知a＞0，b＞0，直线l₁：x+（a-4）y+1=0，l₂：2bx+y-2=0，且l₁⊥l₂，则

  a

  +

  2

  a

  +

  1

  +

  1

  2

  b

  的最小值为（　　）

  A．2

  B．4

  C． 4 5

  D． 9 5
  组卷：1056引用：8难度：0.6

  解析

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

• 21．函数f（x）=Asin（ωx+φ）

  （

  A

  ＞

  0

  ，

  0

  ＜

  ω

  ＜

  16

  ，

  0

  ＜

  φ

  ＜

  π

  2

  ）

  在R上的最大值为

  2

  ，f（0）=1．
  （1）若点

  （

  π

  8

  ，

  2

  ）

  在f（x）的图象上，求函数f（x）图象的对称中心；
  （2）将函数y=f（x）的图象向右平移

  π

  4

  ω

  个单位，再将所得的图象纵坐标不变，横坐标缩小到原来的

  1

  2

  ，得函数y=g（x）的图象，若y=g（x）在

  [

  0

  ，

  π

  8

  ]

  上为增函数，求ω的最大值．
  组卷：474引用：4难度：0.4

  解析

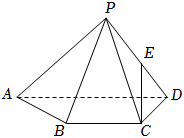• 22．如图，四棱锥P-ABCD中，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB=2，E为PD的中点．
  （1）证明：CE∥平面PAB；
  （2）求直线CE与平面PAB间的距离．
  组卷：549引用：5难度：0.4

  解析