2021-2022学年江苏省连云港市海州区新海初级中学九年级（上）月考数学试卷（12月份）

一、选择题（共8小题，每小题3分，满分24分）

• 1．方程x²-4=0的根为（　　）

  A．2

  B．根号2

  C．±2

  D．±根号2
  组卷：143引用：6难度：0.6

  解析

• 2．已知圆O的半径为5，同一平面内有一点P，且OP=4，则点P与圆O的关系是（　　）

  A．点P在圆内

  B．点P在圆外

  C．点P在圆上

  D．无法确定
  组卷：388引用：8难度：0.5

  解析

• 3．若

  a

  2

  =

  b

  3

  ，则

  2

  a

  -

  b

  a

  +

  b

  =（　　）

  A． 1 5

  B． - 1 5

  C．5

  D．-5
  组卷：22引用：2难度：0.5

  解析

• 4．如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
  

  	甲	乙	丙	丁
  平均数（cm）	180	180	185	185
  方差	8.1	3.6	7.4	3.6

  由表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：24引用：2难度：0.5

  解析

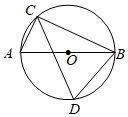• 5．如图，C，D是⊙O上直径AB两侧的两点，设∠ABC=25°，则∠BDC=（　　）

  A．85°

  B．75°

  C．70°

  D．65°
  组卷：2226引用：46难度：0.7

  解析

• 6．筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1．筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2．已知圆心O在水面上方，且⊙O被水面截得的弦AB长为6米，⊙O半径长为4米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（　　）
  

  A．1米

  B．（4- 7 ）米

  C．2米

  D．（4+ 7 ）米
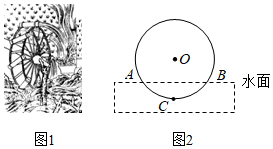  组卷：3208引用：41难度：0.7

  解析

• 7．二次函数y=ax²+bx+c（a≠0）的图象的一部分如图所示．已知图象经过点（-1，0），其对称轴为直线x=1．下列结论：①abc＜0；②4a+2b+c＜0，③3a+c=0；④关于x的方程ax²+bx+c=0（a≠0）的两根分别为-1，3．上述结论中正确结论的个数为（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：21引用：2难度：0.5

  解析

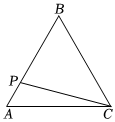• 8．正三角形ABC的边长为2，动点P从点A出发，以每秒1个单位长度的速度，沿A→B→C→A的方向运动，到达点A时停止．设运动时间为x秒，y=PC²，则y关于x的函数的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：26引用：6难度：0.9

  解析

二、填空题（每小题3分，共30分）

• 9．在一个不透明的盒子中，有五个完全相同的小球，把它们分别标号为1，2，3，4，5，随机摸出一个小球，摸出的小球标号为偶数的概率是

   

  ．
  组卷：1059引用：12难度：0.7

  解析

三、解答题（本大题共9小题，共96分．解答时应写出文字说明、证明过程或演算步骤）

• 26．如图，在平面直角坐标系中，给出如下定义：已知点A（2，3），点B（6，3），连接AB．如果线段AB上至少有一个点与点P的距离不大于1，那么称点P是线段AB的“环绕点”．
  
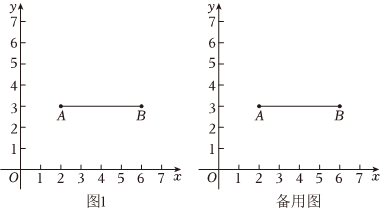
  （1）已知点C（3，1.5），D（4，3.5），E（1，3），则是线段AB的“环绕点”的点是

  ；
  （2）已知点P（m,n）在抛物线y=x²-2x+2上，且点P是线段AB的“环绕点”，求m的取值范围；
  （3）已知⊙M上有一点P是线段AB的“环绕点”，且点M（4，0），求⊙M的半径r的取值范围．
  组卷：18引用：2难度：0.5

  解析

• 27．如图，在平面直角坐标系中，四边形ABCD为正方形，点A，B在x轴上，抛物线y=x²+bx+c经过点B，D（-4，5）两点，且与直线DC交于另一点E．
  
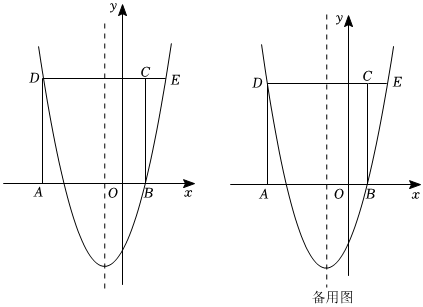
  （1）求抛物线的解析式；
  （2）F为抛物线对称轴与x轴的交点，M为线段DE上一点，N为平面直角坐标系中的一点，若存在以点D、F、M、N为顶点的四边形是菱形．请直接写出点N的坐标，不需要写过程；
  （3）P为y轴上一点，过点P作抛物线对称轴的垂线，垂足为Q，连接OB、BP，探究EQ+PQ+PB是否存在最小值．若存在，请求出这个最小值及点Q的坐标，若不存在，请说明理由．
  组卷：323引用：4难度：0.4

  解析