2022-2023学年江西省抚州市黎川二中高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．复数（1+2i）-（3-4i）对应的点在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：29引用：2难度：0.7

  解析

• 2．已知向量

  a

  =（1，2），

  b

  =（-2，m），若

  a

  与

  b

  共线，则实数m=（　　）

  A．1

  B．-1

  C．4

  D．-4
  组卷：39引用：2难度：0.9

  解析

• 3．在△ABC中，若AD为BC边上的中线，点E在AD上，且AE=2ED，则

  EB

  =（　　）

  A． 2 3 AB - 1 3 AC

  B． 2 3 AC - 1 3 AB

  C． 7 6 AB - 5 6 AC

  D． 7 6 AC - 5 6 AB
  组卷：371引用：15难度：0.8

  解析

• 4．已知直角梯形OABC上下两底分别为分别为2和4，高为

  2

  2

  ，则利用斜二测画法所得其直观图的面积为（　　）

  A． 6 2

  B． 3 2

  C．3

  D．6
  组卷：1143引用：8难度：0.8

  解析

• 5．设f（α）=

  2

  sin

  （

  2

  π

  -

  α

  ）

  cos

  （

  2

  π

  +

  α

  ）

  -

  cos

  （

  -

  α

  ）

  1

  +

  si

  n

  2

  α

  +

  sin

  （

  2

  π

  +

  α

  ）

  -

  co

  s

  2

  （

  4

  π

  -

  α

  ）

  ，则f（-

  23

  6

  π）的值为（　　）

  A． 3 3

  B．- 3 3

  C． 3

  D．- 3
  组卷：421引用：3难度：0.7

  解析

• 6．在△ABC中，已知a=

  3

  ，b=1，A=130°，则此三角形解的情况为（　　）

  A．无解	B．只有一解
  C．有两解	D．解的个数不确定
  组卷：134引用：3难度：0.9

  解析

• 7．在四面体ABCD中，AB⊥平面

  BCD

  ，

  AB

  =

  CD

  =

  2

  ，

  BC

  =

  2

  ，

  ∠

  BCD

  =

  45

  °

  ，则点B到平面ACD的距离为（　　）

  A． 3 7 7

  B． 3 5 5

  C． 2 7 7

  D． 2 5 5
  组卷：44引用：3难度：0.5

  解析

四、解答题（共70分）

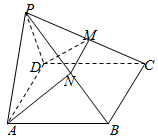• 21．如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，N是PB中点，过A、N、D三点的平面交PC于M．求证：
  （1）PD∥平面ANC；
  （2）M是PC中点．
  组卷：912引用：5难度：0.3

  解析

• 22．已知函数f（x）=sin（

  ωx

  +

  π

  4

  ），g（x）=2sin（

  4

  3

  x

  -

  π

  3

  ）-1，且满足∀x∈[0，π]，f（x）•g（x）≤0恒成立．
  （1）求解g（x）的零点以及f（x）的函数解析式．
  （2）求函数f（x）在区间

  [

  t

  ,

  t

  +

  π

  4

  ]上最大值与最小值之差的取值范围．
  组卷：67引用：2难度：0.4

  解析