2022-2023学年山西省太原十二中九年级（上）月考数学试卷（10月份）

一、选择题

• 1．将一元二次方程（x+3）（2x-1）=-4化为一般形式，结果是（　　）

  A．2x2+5x-7=0

  B．2x2+5x+1=0

  C．2x2-5x+1=0

  D．x2-7x-1=0
  组卷：1129引用：15难度：0.8

  解析

• 2．若关于x的一元二次方程（a+1）x²+x+a²-1=0的一个根是0，则a的值为（　　）

  A．1

  B．-1

  C．±1

  D．0
  组卷：2010引用：26难度：0.9

  解析

• 3．用配方法解方程

  x

  2

  -

  2

  3

  x

  -

  1

  3

  =

  0

  时，应将其变形为（　　）

  A． （ x - 1 3 ） 2 = 2 9

  B． （ x - 2 3 ） 2 = 2 3

  C． （ x - 1 3 ） 2 = 4 9

  D． （ x - 1 3 ） 2 = 0
  组卷：677引用：5难度：0.5

  解析

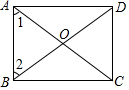• 4．如图，在▱ABCD中，对角线AC与BD交于点O，添加下列条件不能判定▱ABCD为矩形的只有（　　）

  A．AC=BD	B．AB=6，BC=8，AC=10
  C．AC⊥BD	D．∠1=∠2
  组卷：1358引用：14难度：0.7

  解析

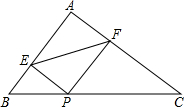• 5．如图，在Rt△ABC中，∠A=90°，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，动点P从点B出发，沿着BC匀速向终点C运动，则线段EF的值大小变化情况是（　　）

  A．一直增大	B．不变
  C．先减小后增大	D．先增大后减小
  组卷：1214引用：10难度：0.5

  解析

• 6．如图，在平面直角坐标系中，Rt△OAB的斜边OA在第一象限，并与x轴的正半轴夹角为30°．C为OA的中点，BC=1，则点A的坐标为（　　）

  A．（ 3 ， 3 ）

  B．（ 3 ，1）

  C．（2，1）

  D．（2， 3 ）
  组卷：1567引用：13难度：0.7

  解析

• 7．若直角三角形的两边长分别是方程x²-7x+12=0的两根，则该直角三角形的面积是（　　）

  A．6

  B．12

  C．12或 3 7 2

  D．6或 3 7 2
  组卷：3515引用：33难度：0.6

  解析

二、

• 21．邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作，在余下的四边形纸片中再剪去一个菱形，余下一个四边形，称为第二次操作，…依此类推，若第n次余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图，▱ABCD中，若AB=1，BC=2，则▱ABCD为1阶准菱形；▱EFGH中，若EH=4x,EF=3x,则▱EFGH为3阶准菱形．
  （1）判断与推理：
  邻边长分别为2和3的平行四边形是

  阶准菱形；
  （2）操作、探究、计算：
  ①已知▱ABCD的边长分别为1，a（a＞1）且是3阶准菱形，请画出▱ABCD及裁剪线的示意图，并在下方写出的a值．
  ②已知▱ABCD的邻边长分别为a,b（a＞b），满足a=3b+m,b=4m,请写出▱ABCD是

  阶准菱形．
  
  组卷：263引用：5难度：0.4

  解析

• 22．（1）如图1，将矩形ABCD折叠，使AB落在对角线AC上，折痕为AE，点B落在B₁处，若∠DAC=66°，则∠BAE=

  °；
  （2）小丽手中有一张矩形纸片，AB=9，AD=4．她准备按如下两种方式进行折叠：
  ①如图2，点F在这张矩形纸片的边CD上，将纸片折叠，使点D落在边AB上的点D₁处，折痕为FG，若DF=5，求AG的长；
  ②如图3，点H在这张矩形纸片的边AB上，将纸片折叠，使HA落在射线HC上，折痕为HK，点A，D分别落在A₁，D₂处，若DK=

  7

  3

  ，求A₁C的长．
  
  组卷：971引用：4难度：0.3

  解析