2022-2023学年广西贵港市港南区八年级(下)期末数学试卷
发布:2024/6/6 8:0:9
一、选择题:(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个是正确的,每小题选对得3分,选错、不选、或多选均得零分)
-
1.平面直角坐标系中,在第二象限的点是( )
组卷:235引用:3难度:0.8 -
2.一本笔记本5元,买x本共付y元,则变量是( )
组卷:1031引用:15难度:0.8 -
3.下列图形是中心对称图形的是( )
组卷:139引用:5难度:0.9 -
4.某同学在做“投掷一枚正方体骰子”的实验时,连续抛了10次,共有3次掷得数字“4”,则掷得数字“4”的频率是( )
组卷:206引用:3难度:0.8 -
5.已知直角三角形中30°角所对的直角边长是2cm,则另一条直角边长为( )cm.
组卷:124引用:2难度:0.8 -
6.某登山队大本营所在地的气温为8℃.海拔每升高1km,气温下降6℃.队员由大本营向上登高x km,气温为y℃,则y与x的函数关系式为( )
组卷:386引用:8难度:0.8 -
7.下列各组数中不能作为直角三角形的三边长的是( )
组卷:188引用:3难度:0.8 -
8.在平面直角坐标系中,点P(-2,3)关于x轴对称点的坐标为( )
组卷:329引用:7难度:0.7
三、解答题:(本大题共8小题,满分72分)
-
25.“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
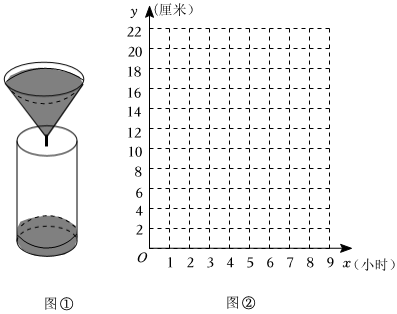
(1)表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
在如图②所示的直角坐标系中描出上表的各点,用光滑的线连接;时间x(小时) 1 2 3 4 5 圆柱体容器液面高度y(厘米) 6 10 14 18 22
(2)请根据(1)中的数据确定y与x之间的函数表达式;
(3)如果本次实验记录的开始时间是上午9:00,那么当圆柱体容器液面高度达到12厘米时是几点?组卷:1254引用:16难度:0.6 -
26.在数学实践活动课上,“卓越”小组准备研究如下问题:如图,EF为直尺的一条边,四边形ABCD为一正方形纸板(∠DAB、∠ABC、∠BCD、∠D均为直角)
(1)【操作发现】
如图①小组成员小方把正方形的一条边AB与EF重合放置,刘老师在与同学们交流研讨时又做出了∠DAF的平分线AQ,交正方形的边于点P.
则此时∠PAB的度数为 ;∠PAB与∠DAE的度数之间的关系为 .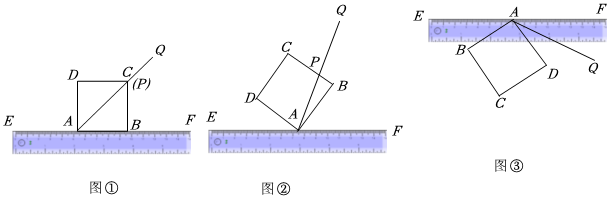
(2)【问题探究】
受小方同学的启发,小组成员小丽将正方形纸板按如图②放置,若此时记∠DAE的度数为α,其他条件不变,请帮小丽同学探究:∠PAB与∠DAE的度数之间的关系是否发生改变,并说明理由.
(3)【拓展延伸】
组内其他同学也都继续探索,将正方形按如图③放置,刘老师同样做出了∠DAF的平分线AQ,请直接写出∠QAB与∠DAE的度数之间的关系.组卷:752引用:7难度:0.6


