当前位置：试卷中心 > 试卷详情

2022-2023学年吉林省普通高中友好学校第三十六届联合体高一（下）期中数学试卷

发布：2024/6/16 8:0:10

1．已知复数z满足（1-i）z=2+i,i是虚数单位，则z=（　　）
A．
1
2
+
3
2
i
B．
-
1
2
-
3
2
i
C．
1
2
-
3
2
i
D．
-
1
2
+
3
2
i
组卷：13引用：2难度：0.8
解析
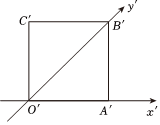2．一个平面图形用斜二测画法画出的直观图如图所示，此直观图恰好是一个边长为2的正方形，则原平面图形的周长为（　　）
A．8 B．
4
+
4
3
C．16 D．
8
+
8
3
组卷：97引用：5难度：0.7
解析
3．在△ABC中，内角A，B，C的对边分别为a,b,c,a=2，
b
=
7
，B=60°，则c=（　　）
A．1 B．
3
C．3 D．1或3
组卷：126引用：5难度：0.7
解析
4．圆锥侧面展开图扇形的圆心角为60°，底面圆的半径为8，则圆锥的侧面积为（　　）
A．384π B．392π C．398π D．404π
组卷：356引用：6难度：0.7
解析
5．已知△ABC，
BD
=
2
DC
，E为AD的中点，记
AB
=
a
，
AC
=
b
，则
BE
=（　　）
A．
-
5
6
a
-
1
3
b
B．
-
5
6
a
+
1
3
b
C．
-
2
3
a
-
1
6
b
D．
-
2
3
a
+
1
6
b
组卷：16引用：2难度：0.8
解析
6．已知向量
a
，
b
满足
（
a
+
b
）
•
b
=
2
，且
|
b
|
=
1
，则向量
a
在向量
b
上的投影向量为（　　）
A．1 B．-1 C．
b
D．
-
b
组卷：315引用：7难度：0.8
解析
7．在正四棱锥S-ABCD中，底面是边长为2的正方形，侧面是腰长为
6
的等腰三角形，则正四棱锥S-ABCD的外接球的体积为（　　）
A．
27
π
2
B．9π C．
9
π
2
D．18π
组卷：258引用：3难度：0.6
解析

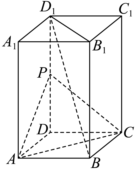21．如图，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是菱形，AA₁⊥平面ABCD，AB=1，AA₁=2，∠BAD=60°，点P为DD₁的中点．
（1）求证：直线BD₁∥平面PAC；
（2）求二面角B₁-AC-P的余弦值．
组卷：317引用：5难度：0.5
解析
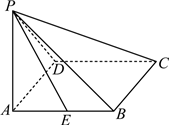22．如图所示，四边形ABCD为菱形，PA=PD，平面PAD⊥平面ADC，点E是棱AB的中点．
（1）求证：PE⊥AC；
（2）若PA=AB=BD=2，求三棱锥E-PCD的体积；
（3）若PA=AB，当二面角P-AC-B的正切值为-2时，求直线PE与平面ABCD所成的角．
组卷：61引用：4难度：0.5
解析