2022-2023学年河北省邢台市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．

  1

  +

  2

  i

  1

  -

  3

  i

  =（　　）

  A． 1 2 + 1 2 i

  B． - 1 2 + 1 2 i

  C． 1 2 - 1 2 i

  D． - 1 2 - 1 2 i
  组卷：63引用：12难度：0.8

  解析

• 2．若一组数据为1，3，4，6，7，10，13，则这组数据的第70百分位数为（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：69引用：2难度：0.9

  解析

• 3．在三棱锥A-BCD中，△ABC，△BCD均为等边三角形，BC=2，∠ACD=90°，M为AD的中点，则异面直线AB与CM所成角的余弦值为（　　）

  A．0

  B． 2 2

  C． 3 2

  D．1
  组卷：156引用：7难度：0.5

  解析

• 4．A队共有甲、乙两名队员回答某道题，有1人答出则此题回答正确，甲答出的概率为

  1

  5

  ，乙答出的概率为

  1

  6

  ，则此题A队回答正确的概率是（　　）

  A． 2 15

  B． 1 6

  C． 1 3

  D． 1 2
  组卷：36引用：3难度：0.8

  解析

• 5．某校高一、高二、高三年级的学生人数分别为1200，1000，800，按年级进行分层，用分层随机抽样的方法抽取一个容量为30的样本，调查全校学生的睡眠时间．高一年级抽取的学生的平均睡眠时间为8.5小时，高二年级抽取的学生的平均睡眠时间为7.8小时，三个年级抽取的学生的总平均睡眠时间为8小时，则高三年级抽取的学生的平均睡眠时间为（　　）

  A．7.2小时

  B．7.3小时

  C．7.5小时

  D．7.6小时
  组卷：62引用：2难度：0.8

  解析

• 6．在平行四边形ABCD中，∠A=60°，AB=1，AD=2，将△ABD沿BD折起，使得平面ABD⊥平面BCD，则B到平面ACD的距离为（　　）

  A． 3 3

  B． 2 2

  C． 5 3

  D． 3 2
  组卷：132引用：8难度：0.5

  解析

• 7．已知△ABC的外接圆为圆O，圆O的直径AB=10，且

  AB

  •

  AC

  =

  64

  ，则

  CO

  •

  CA

  =（　　）

  A．80

  B．64

  C．48

  D．32
  组卷：28引用：2难度：0.8

  解析

四、解答题：本题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤.

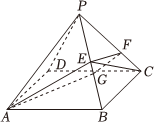• 21．已知四棱锥P-ABCD的体积为1，底面ABCD为平行四边形，E，F分别是PB，PC上的点，PE=EB，PF=2FC，平面AEF交CD于点G．
  （1）求

  DG

  GC

  ；
  （2）求多面体ABCGFE的体积．
  组卷：21引用：2难度：0.4

  解析

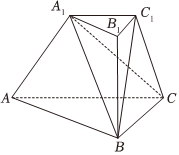• 22．如图，在三棱台ABC-A₁B₁C₁中，BB₁⊥平面ABC，∠ABC=90°，AB=BC=4，A₁B₁=2，BB₁=

  2

  2

  ．
  （1）证明：BC₁⊥A₁C；
  （2）求A₁B与平面ACC₁A₁所成角的正弦值．
  组卷：296引用：7难度：0.6

  解析