2022-2023学年陕西省西安市西工大附中高一(下)第二次月考数学试卷
发布:2024/7/17 8:0:9
一、单项选择题:本大题共8小题,每小题3分,共24分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.已知复数z=1-2i,则z的虚部为( )
组卷:123引用:8难度:0.9 -
2.某工厂生产A、B、C三种不同型号的产品,新产品数量之比依次为k:5:3,现用分层抽样的方法抽出一个容量为120的样本,已知A种产品共抽取了24件,则C种型号产品抽取的件数为( )
组卷:725引用:18难度:0.9 -
3.已知α,β是两个不重合的平面,在下列条件中,可判断平面α,β平行的是( )
组卷:1705引用:8难度:0.7 -
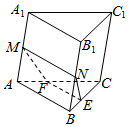 4.如图,在三棱柱ABC-A1B1C1中,M,N分别为棱AA1,BB1的中点,过MN作一平面分别交底面三角形ABC的边BC,AC于点E,F,则( )组卷:341引用:5难度:0.7
4.如图,在三棱柱ABC-A1B1C1中,M,N分别为棱AA1,BB1的中点,过MN作一平面分别交底面三角形ABC的边BC,AC于点E,F,则( )组卷:341引用:5难度:0.7 -
5.设A,B为锐角三角形的两个内角,则复数z=(cosB-sinA)+itanB对应的点位于复平面的( )
组卷:31引用:2难度:0.7 -
6.设PA垂直于△ABC所在的平面α,∠BAC=90°,PB、PC分别与α成45°和30°角,PA=2,点P到BC的距离是( )
组卷:43引用:2难度:0.5 -
7.已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形且边长为1,侧棱AA1长为2,以A1为球心,
为半径的球面与侧面CDD1C1的交线长为( )3组卷:174引用:4难度:0.3
三、解答题(本大题共4小题,每小题10分,共40分。解答应写出文字说明、证明过程或演算步骤)
-
21.如图,在矩形ABCD中,AB=2AD=4,M,N分别是AB和CD的中点,P是BM的中点.将矩形AMND沿MN折起,形成多面体AMB-DNC.
(1)证明:BD∥平面ANP;
(2)若二面角A-MN-B大小为120°,求直线AP与平面ABCD所成角的正弦值.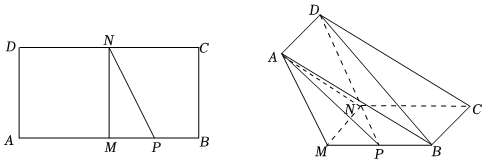 组卷:155引用:2难度:0.5
组卷:155引用:2难度:0.5 -
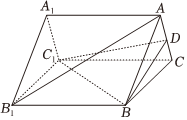 22.已知正三棱柱ABC-A1B1C1中,AB=4,D为AC边的中点,AB1⊥BC1.
22.已知正三棱柱ABC-A1B1C1中,AB=4,D为AC边的中点,AB1⊥BC1.
(1)求侧棱长;
(2)求三棱锥D-BCC1的体积;
(3)求二面角D-BC1-C的大小.组卷:49引用:2难度:0.5


