2023-2024学年四川省成都实验外国语学校（西区）九年级（上）月考数学试卷（10月份）

一.选择题（每小题4分，共32分）

• 1．下列是一元二次方程的是（　　）

  A．2x+1=0

  B．y2+x=1

  C． 1 x =1

  D．x2+2x+7=0
  组卷：132引用：7难度：0.8

  解析

• 2．若关于x的一元二次方程（k-2）x²+x+k²-4=0有一个根是0，则k的值是（　　）

  A．-2

  B．2

  C．0

  D．-2或2
  组卷：5346引用：33难度：0.5

  解析

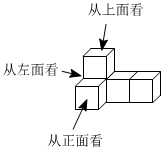• 3．如图是由5个完全相同的小正方体搭成的几何体，从左面看得到的平面图形是（　　）

  A．

  B．

  C．

  D．
  组卷：248引用：7难度：0.8

  解析

• 4．下列说法中，正确的是（　　）

  A．对角线互相垂直且相等的四边形是正方形

  B．对角线互相平分的四边形是菱形

  C．对角线互相垂直的四边形是平行四边形

  D．对角线相等的平行四边形是矩形
  组卷：2449引用：15难度：0.9

  解析

• 5．一个不透明的箱子里共装有m个球，其中红球4个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.4附近，则可以估算出m的值为（　　）

  A．4

  B．6

  C．10

  D．12
  组卷：194引用：2难度：0.5

  解析

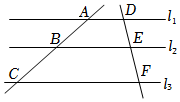• 6．如图，直线l₁∥l₂∥l₃，直线AC和DF被l₁，l₂，l₃所截，AB=5，BC=6，EF=4，则DE的长为（　　）

  A．2

  B．3

  C．4

  D． 10 3
  组卷：1505引用：87难度：0.7

  解析

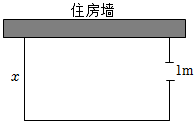• 7．一花户，有26m长的篱笆，要围成一边靠住房墙（墙长12m）的面积为80m²的长方形花园，且垂直于住房墙的一边留一个1m的门（如图），设垂直于住房墙的其中一边长为xm,则可列方程为（　　）

  A．x （ 27 - x 2 ） =80	B．x（26-2x）=80
  C．x （ 26 - x 2 ） =80	D．x（27-2x）=80
  组卷：2162引用：18难度：0.7

  解析

• 8．如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为

  1

  3

  ，点A，B，E在x轴上，若正方形BEFG的边长为12，则C点坐标为（　　）

  A．（6，4）

  B．（6，2）

  C．（4，4）

  D．（8，4）
  组卷：2294引用：21难度：0.7

  解析

五、解答题

• 25．如图1，在平面直角坐标系xOy中，点A（-1，0），B（4，0），点C在y轴的负半轴上，连接AC，BC，满足∠ACO=∠CBO．
  （1）求直线BC的解析式；
  （2）如图2，已知直线l₁：

  y

  =

  3

  2

  x

  -

  6

  经过点B．
  ①若点D为直线l₁上一点，直线AD与直线BC交于点H，若

  S

  △

  BDH

  S

  △

  ABH

  =

  2

  3

  ，求点D的坐标；
  ②过点O作直线l₂∥BC，若点M、N分别是直线l₁和l₂上的点，且满足∠ABC=∠MNB．请问是否存在这样的点M、N，使得△ABC与△MBN相似？若存在，请直接写出点N的坐标；若不存在，请说明理由．
  
  组卷：847引用：6难度：0.1

  解析

• 26．【模型发现】如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），过点D作垂直于AE的一条直线DF，垂足为G，交AB于点F．小明发现可以通过证明：△DAF≌△ABE得AE=DF．（不需证明）
  【模型探究】（1）如图2，在正方形ABCD中，P为边BC上一点（不与点B、C重合），M为线段CD上一点（不与C、D重合），过点M作MN⊥AP，垂足为G，交AB于点N，请直接写出线段DM、BN、CP之间的数量关系．
  （2）如图3，在（1）的条件下，若垂足G恰好为AP的中点，连接BD，交MN于点H，连接PH并延长交边AD于点I，再连接BG，请探究线段BG、GH的数量关系；
  【拓展应用】（3）如图4，若正方形ABCD的边长为8，点M、N分别为边CD、AB上的点，过点A作AG⊥MN，已知AG=5，将正方形ABCD沿着MN翻折，BC的对应边B'C′恰好经过点A，连接C'M交AD于点Q．过点Q作QR⊥MN，垂足为R，求线段QR的长．（直接写出结论即可）
  
  组卷：400引用：1难度：0.3

  解析