当前位置：试卷中心 > 试卷详情

2023-2024学年黑龙江省哈尔滨市香坊区风华中学九年级（上）段考数学试卷（10月份）（五四学制）

发布：2024/9/25 4:0:1

一、选择题（3×8=24分）

1．下列各式中是二次函数的是（　　）
A．
y
=
1
x
2
+
2
x
B．y=（x-1）²-1
C．y=x（x+1）-x² D．y=ax²+bx+c
组卷：140引用：3难度：0.7
解析
2．在Rt△ABC中，∠C=90°，若
AB
=
5
，AC=1，则tanB的值为（　　）
A．
1
2
B．2 C．
5
5
D．
2
5
5
组卷：576引用：5难度：0.6
解析
3．将抛物线y=-（x-1）²+3向左平移1个单位长度，再向上平移3个单位长度，得到抛物线的解析式是（　　）
A．y=-（x-2）²+6 B．y=-（x-2）²
C．y=-x² D．y=-x²+6
组卷：25引用：1难度：0.5
解析
4．在Rt△ABC中，∠C=90°，
tan
A
=
3
4
．则cosA的值为（　　）
A．
3
7
7
B．
4
5
C．
4
7
7
D．
3
5
组卷：445引用：2难度：0.7
解析
5．已知抛物线的解析式为
y
=
-
2
3
（
x
+
3
）
2
-
2
，则该抛物线的顶点坐标是（　　）
A．（3，2） B．（-3，2） C．（-3，-2） D．（3，-2）
组卷：40引用：1难度：0.5
解析
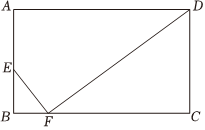6．如图，点E、F分别在矩形ABCD的边AB、BC上，且∠EFD=90°，若BF=3，BE=4，CD=9，则FC的长为（　　）
A．12 B．13 C．14 D．15
组卷：19引用：4难度：0.7
解析
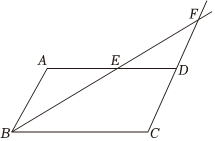7．如图，点E是平行四边形ABCD的边AD上一点，射线BE交CD延长线于点F，则下列结论错误的是（　　）
A．
AE
DE
=
CD
DF
B．
DF
FC
=
EF
BF
C．
AB
FD
=
AE
AD
D．
BE
BF
=
AB
CF
组卷：74引用：1难度：0.6
解析
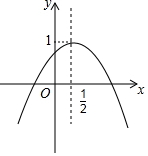8．如图，二次函数y=ax²+bx+c的图象与y轴正半轴相交，其顶点坐标为（
1
2
，1），下列结论：①abc＜0；②b²-4ac＞0；③a+b+c＜0；④a+b=0；⑤a-b+c＜0．其中一定正确的个数是（　　）
A．2个 B．3个 C．4个 D．5个
组卷：467引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共72分）

23．综合与实践
数学是以数量关系和空间形式为主要研究对象的科学，数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系，让我们在学习与探索中发现数学的美，体会数学实践活动带给我们的乐趣．
转一转：如图①，在矩形ABCD中，点E、F、G分别为边BC、AB、AD的中点，连接EF、DF，H为DF的中点，连接GH．将△BEF绕点B旋转，线段DF、GH和CE的位置和长度也随之变化．
当△BEF绕点B顺时针旋转90°时，请解决下列问题：
（1）图②中，AB=BC，此时点E落在AB的延长线上，点F落在线段BC上，连接AF，猜想GH与CE之间的数量关系，并证明你的猜想；
（2）图③中，AB=2，BC=3，则
GH
CE
=
；
（3）当AB=m,BC=n时，
GH
CE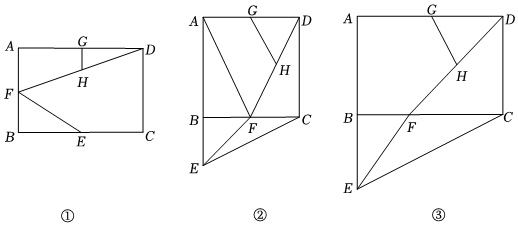
=
．

剪一剪、折一折：（4）在（2）的条件下，连接图③中矩形的对角线AC，并沿对角线AC剪开，得△ABC（如图④）．点M、N分别在AC、BC上，连接MN，将△CMN沿MN翻折，使点C的对应点P落在AB的延长线上，若PM平分∠APN，则CM长为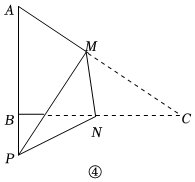
．
组卷：1760引用：7难度：0.1
解析
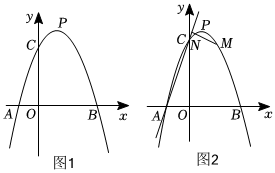24．已知抛物线y=-x²+bx+c（b,c为常数，-9＜c＜9）的顶点为P，与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C（点C与点A不重合），抛物线上的点M的横坐标为m,且
b
2
＜m＜3，过点M作MN⊥直线AC，垂足为N．
（1）若b=2，c=3．
①如图1，求点A、B、C和点P的坐标；
②如图2，当MN=
3
5
10
时，求点M的坐标；
（2）若点A的坐标为
（
-
c
3
，
0
）
且PM∥BC，当AN+3MN=
9
2
10
时，求点M的坐标．
组卷：83引用：1难度：0.2
解析