2022-2023学年黑龙江省双鸭山一中高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．若复数z满足z（2-i）=5，则z的共轭复数的虚部为（　　）

  A．-1

  B．0

  C．-i

  D．1
  组卷：102引用：3难度：0.8

  解析

• 2．已知向量

  a

  ，

  b

  满足：

  ＜

  a

  ，

  b

  ＞

  =

  60

  °

  ，

  |

  a

  |

  =

  1

  ，

  b

  =

  （

  1

  ，-

  3

  ）

  ，则

  |

  2

  a

  -

  b

  |

  =（　　）

  A．0

  B．2

  C．4

  D． 2
  组卷：251引用：2难度：0.7

  解析

• 3．设m,n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：
  ①若m∥α，α⊥β，则m⊥β；
  ②若m⊥β，m∥α，则α⊥β；
  ③若α∩β=m,m∥γ，则α∥γ，β∥γ；
  ④若α⊥γ，β⊥γ，则α∥β．
  则真命题为（　　）

  A．②③

  B．③④

  C．②

  D．②④
  组卷：86引用：3难度：0.7

  解析

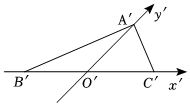• 4．如图为△ABC水平放置的直观图，其中B′O′=C′O′=1，

  A

  ′

  O

  ′

  =

  3

  2

  ，那么原△ABC的面积是（　　）

  A． 3

  B． 2 3

  C． 3 2

  D．2
  组卷：457引用：5难度：0.9

  解析

• 5．甲、乙两人在一次射击比赛中各射靶5次，两人成绩的条形统计图如图所示，则（　　）
  

  A．甲的成绩的平均数小于乙的成绩的平均数

  B．甲的成绩的中位数等于乙的成绩的中位数

  C．甲的成绩的方差小于乙的成绩的方差

  D．甲的成绩的极差小于乙的成绩的极差
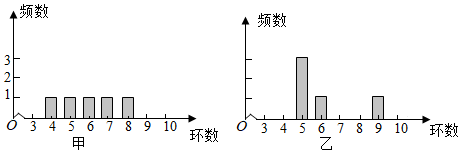  组卷：840引用：36难度：0.9

  解析

• 6．直三棱柱ABC-A₁B₁C₁的各顶点都在同一球面上，若AB=AC=AA₁=2，∠BAC=120°，则此球的表面积等于（　　）

  A．20π

  B．10π

  C．5π

  D．5 5 π
  组卷：572引用：8难度：0.7

  解析

• 7．已知圆锥的高为1，体积为π，则过圆锥顶点作圆锥截面的面积最大值为（　　）

  A． 3

  B．2

  C． 2 3 π

  D．3π
  组卷：103引用：3难度：0.5

  解析

四、解答题（共70分）

• 22．已知△ABC是锐角三角形，内角A，B，C所对的边分别为a,b,C，面积为S，bsinA=acos（B-

  π

  6

  ）．
  （1）求角B；
  （2）若a=2，求s的取值范围．
  组卷：84引用：4难度：0.5

  解析

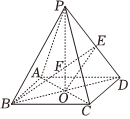• 23．如图所示，在正四棱锥P-ABCD中，底面ABCD的中心为O，BE⊥PD于E，BE与PO交点为F，PF=2FO．
  （1）求证：EO∥平面PAB．
  （2）求二面角P-AB-E的正弦值．
  
  组卷：113引用：3难度：0.5

  解析