2022-2023学年浙江省湖州市南浔区八年级（下）期末数学试卷

一、选择题（本题有10小题，每小题3分，共30分）

• 1．下列方程中是一元二次方程的是（　　）

  A．x2+1=0

  B．x2+y=1

  C．2x+1=0

  D． 1 x + x 2 = 1
  组卷：216引用：2难度：0.8

  解析

• 2．下列用数学家命名的图形中，是中心对称图形的是（　　）

  A． 笛卡尔心形线	B． 谢尔宾斯基地毯
  C． 赵爽弦图	D． 斐波那契螺旋线
  组卷：158引用：4难度：0.9

  解析

• 3．方差是刻画一组数据波动大小的量，对于一组数据x₁，x₂，x₃，…，x_n，可用如下算式计算方差：S²=

  1

  n

  [（x₁-3）²+（x₂-3）²+（x₃-3）²+…+（x_n-3）²]，其中“3”是这组数据的（　　）

  A．最小值

  B．平均数

  C．众数

  D．中位数
  组卷：536引用：10难度：0.9

  解析

• 4．若反比例函数

  y

  =

  k

  x

  （

  k

  ≠

  0

  ）

  的图象经过点（3，-2），则该反比例函数的图象在（　　）

  A．第一、二象限	B．第一、三象限
  C．第二、三象限	D．第二、四象限
  组卷：54引用：1难度：0.5

  解析

• 5．下列各式中，是最简二次根式的是（　　）

  A． 2

  B． 1 5

  C． 27

  D． a 2
  组卷：429引用：4难度：0.8

  解析

• 6．用反证法证明“在△ABC中，若AB≠AC，则∠B≠∠C”时，第一步应假设（　　）

  A．AB=AC

  B．AB≠AC

  C．∠B=∠C

  D．∠B≠∠C
  组卷：315引用：6难度：0.7

  解析

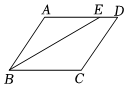• 7．如图，已知在▱ABCD中，∠ABC的平分线BE交AD于点E．∠AEB=25°，则∠A的度数是（　　）

  A．150°

  B．120°

  C．100°

  D．130°
  组卷：42引用：1难度：0.8

  解析

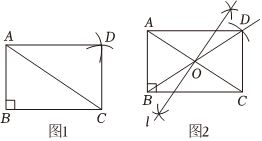• 8．已知：Rt△ABC中．∠ABC=90°，求作：矩形ABCD．以下是甲、乙两同学的作业：
  甲：1．以点C为圆心，AB为半径画弧；2．以点A为圆心，BC为半径画弧；3．两弧在BC上方交于点D，连接AD、CD．四边形ABCD即为所求（如图1）．
  乙：1．分别以点A、C为圆心，大于

  1

  2

  AC

  的长为半径画弧，相交于点E、F，作直线EF，交线段AC于点O；2．作射线BO，在BO上截取OD，使OD=OB；3．连接AD、CD．四边形ABCD即为所求（如图2）．
  对于两人的作业，下列说法正确的是（　　）

  A．甲对，乙不对	B．甲不对，乙对
  C．两人都对	D．两人都不对
  组卷：82引用：1难度：0.5

  解析

三、解答题（本题有8小题，共66分）

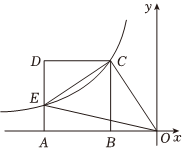• 23．如图，在平面直角坐标系xOy中，点A和点B在x轴的负半轴上，OB=m,AB=4，以线段AB为边向上作正方形ABCD，反比例函数

  y

  =

  k

  x

  （

  x

  ＜

  0

  ，

  k

  ＜

  0

  ）

  的图象经过顶点C，且与边AD相交于点E．
  （1）当m=4时，求k的值及点E的坐标；
  （2）连接OC，CE，OE．
  ①若△COE的面积为

  48

  5

  ，求该反比例函数的表达式；
  ②是否存在某一位置，使得OC⊥CE，若存在，请求出m的值；若不存在，请说明理由．
  组卷：472引用：1难度：0.5

  解析

• 24．如图，已知在菱形ABCD中．∠DAB=60°，AB=6，对角线AC与BD交于点O，点E是射线AC上的一个动点，将线段DE绕点D顺时针旋转120°，得到线段DF，连接EF，AF，BE．
  （1）如图1，当点E在线段AC上运动时，
  ①求证：△ADF≌△CDE；
  ②当BE∥AF时，判断四边形ABEF的形状，并说明理由．
  （2）在点E的整个运动过程中，将△CDE沿着DE翻折得到四边形CDC′E，当四边形CDC′E为菱形时，求出此时△AEF的面积．
  
  组卷：445引用：1难度：0.1

  解析