2022-2023学年上海市闵行区莘庄中学高一（下）期中数学试卷

一.填空题（本大题共12题，满分54分，第1～6题每题4分，第7～12题每题5分）

• 1．若扇形的圆心角为

  2

  π

  3

  ，半径为2，则扇形的面积为

  ．
  组卷：236引用：13难度：0.8

  解析

• 2．函数f（x）=1-cos²x的最小正周期为

  ．
  组卷：33引用：1难度：0.7

  解析

• 3．已知

  cosα

  =

  3

  5

  且tanα＜0，则

  cos

  （

  3

  π

  2

  +

  α

  ）

  =

  ．
  组卷：65引用：2难度：0.7

  解析

• 4．已知

  |

  a

  |

  =

  2

  ，

  （

  2

  a

  -

  b

  ）

  ⊥

  a

  ，则

  b

  在

  a

  向上的数量投影为

  ．
  组卷：132引用：4难度：0.8

  解析

• 5．已知角α的终边经过点P（-4，3），则cos（π-2α）=

  ．
  组卷：43引用：1难度：0.8

  解析

• 6．在△ABC中，若a=4，B=60°，其面积为

  3

  3

  ，则b的值为

  ．
  组卷：149引用：2难度：0.7

  解析

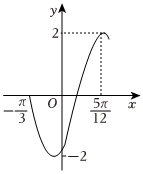• 7．函​数f（x）=Asin（ωx+φ）（A＞0，ω＞0，

  |

  φ

  |

  ＜

  π

  2

  ）的部分图像如图所示，则f（x）=

  ．
  组卷：120引用：1难度：0.8

  解析

三.解答题（本大题共5题，共14+15+15+16+18=78分）

• 20．已知函数

  f

  （

  x

  ）

  =

  msinx

  +

  2

  cosx

  ．
  （1）若m＞0且f（x）的最大值为2，求函数y=f（x）在

  [

  0

  ，

  π

  2

  ]

  上的单调递增区间；
  （2）若m=0，函数

  y

  =

  f

  （

  x

  ）

  +

  f

  （

  x

  +

  π

  2

  ）

  -

  t

  在

  [

  -

  π

  2

  ，

  π

  2

  ]

  上有且仅有一个零点，求实数t的取值范围；
  （3）已知y=f（x）的一条对称轴方程为

  x

  =

  π

  4

  ，令F（x）=（x-6）²•f（ωx），存在常数a∈R，使得函数y=F（x+a）为偶函数，求最小的正数ω的值．
  组卷：53引用：1难度：0.5

  解析

• 21．已知函数f（x）=sin（2x+φ）（0＜φ＜π）．
  （1）当

  φ

  =

  π

  4

  时，求函数y=f（x）的最大值，并求出取得最大值时所有x的值；
  （2）若f（x）为偶函数，设

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  -

  f

  （

  x

  +

  π

  6

  ）

  ，若不等式|g（x）-m|＜2在

  x

  ∈

  [

  0

  ，

  π

  2

  ]

  上恒成立，求实数m的取值范围；
  （3）若f（x）过点

  （

  π

  6

  ，

  1

  ）

  ，设h（x）=cos²x+2asinx,若对任意的

  x

  1

  ∈

  [

  -

  π

  2

  ，

  π

  2

  ]

  ，

  x

  2

  ∈

  [

  0

  ，

  π

  2

  ]

  ，都有h（x₁）＜f（x₂）+3，求实数a的取值范围．
  组卷：98引用：6难度：0.4

  解析