2022-2023学年湖南省张家界市慈利一中高三（上）第四次月考数学试卷

一、单选题（本题共8小题，每小题5分，共40分）

• 1．设集合A={x|-1≤x≤2}，B={y|y=2^x，x∈A}，则A∩B=（　　）

  A．[-1，2]

  B．（0，2]

  C．[-1，4]

  D． [ 1 2 ， 2 ]
  组卷：7引用：3难度：0.7

  解析

• 2．设复数z=

  1

  1

  -

  i

  ，

  z

  是z的共轭复数，则z+

  z

  =（　　）

  A． 1 + i 2

  B．i

  C．-1

  D．1
  组卷：9引用：7难度：0.9

  解析

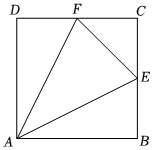• 3．如图，在正方形ABCD中，E，F分别为边BC，CD的中点，若

  EF

  =

  λ

  AD

  +

  μ

  AE

  ，则λ+μ=（　　）

  A．-2

  B． 3 4

  C． 1 4

  D．4
  组卷：16引用：4难度：0.8

  解析

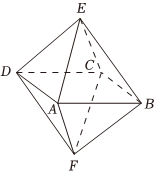• 4．如图是一个正八面体，其每一个面都是正三角形，六个顶点都在球O的球面上，则球O与正八面体的体积之比是（　　）

  A．π

  B． 4 π 3

  C． 3 π 2

  D．2π
  组卷：9引用：2难度：0.7

  解析

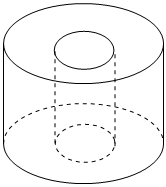• 5．如图，某种卷筒卫生纸绕在圆柱形盘上，空盘时盘芯直径为40mm,满盘时直径为120mm,已知卫生纸的厚度为0.1mm,则满盘时卫生纸的总长度大约（π≈3.14，精确到1m）（　　）

  A．60m

  B．80m

  C．100m

  D．120m
  组卷：101引用：4难度：0.6

  解析

• 6．记函数

  f

  （

  x

  ）

  =

  cos

  （

  ωx

  +

  π

  3

  ）

  +

  b

  （

  ω

  ＞

  0

  ）

  的最小正周期为T，若

  π

  ＜

  T

  ＜

  3

  π

  2

  ，且（π，2）是y=f（x）图象的一个最高点，则

  f

  （

  π

  4

  ）

  =（　　）

  A． 1 - 2 2

  B． 1 + 2 2

  C． 2 - 2 2

  D． 2 + 2 2
  组卷：194引用：3难度：0.6

  解析

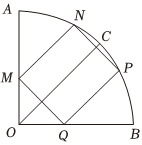• 7．慈利一中为提质升级，改善办学条件，如图所示，校体育馆边有一块扇形空地AOB，其半径为20m,∠AOB=90°，C为弧AB的中点，要在其内接矩形MNPQ（点M、Q分别在半径OA、OB上，点N、P在弧AB上，且MN∥OC）上修建一栋新教学楼，则占地面积的最大值为（单位：m²）（　　）

  A．50π

  B．25π

  C． 400 （ 2 - 1 ）

  D． 400 2
  组卷：15引用：1难度：0.5

  解析

四、解答题（本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）

• 21．椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦点分别为F₁，F₂，焦距为2

  2

  ，点M为椭圆上位于x轴上方的一点，满足

  M

  F

  1

  •

  M

  F

  2

  =0，且△MF₁F₂的面积为2．
  （1）求椭圆C的方程；
  （2）设椭圆C的左、右顶点分别为A，B，直线l交椭圆C于P，Q两点，记直线AP的斜率为k₁，直线BQ的斜率为k₂，已知k₁=2k₂.过点B作直线PQ的垂线，垂足为H，问：在平面内是否存在定点T，使得|TH|为定值，若存在，求出点T的坐标；若不存在，试说明理由．
  组卷：145引用：2难度：0.3

  解析

• 22．已知函数f（x）=nx-xⁿ，x∈R，其中n∈N^•，且n≥2．
  （Ⅰ）讨论f（x）的单调性；
  （Ⅱ）设曲线y=f（x）与x轴正半轴的交点为P，曲线在点P处的切线方程为y=g（x），求证：对于任意的正实数x,都有f（x）≤g（x）；
  （Ⅲ）若关于x的方程f（x）=a（a为实数）有两个正实数根x₁，x₂，求证：|x₂-x₁|＜

  a

  1

  -

  n

  +2．
  组卷：5548引用：13难度：0.1

  解析