2023-2024学年四川省成都市锦江区名校高三（上）开学数学试卷（理科）

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求的．

• 1．已知集合A={x|x²+2x≤0}，

  B

  =

  {

  a

  |

  ∃

  x

  ∈

  R

  ，

  x

  2

  -

  ax

  +

  1

  4

  ＜

  0

  }

  ，则A∩B=（　　）

  A．[1，2）

  B．[-2，-1]

  C．[-2，1）

  D．[-2，-1）
  组卷：57引用：3难度：0.8

  解析

• 2．复数z在复平面内对应的点为（2，1），则

  2

  i

  z

  -

  1

  =（　　）

  A．1+i

  B．1-i

  C．-1+i

  D．-1-i
  组卷：221引用：9难度：0.8

  解析

• 3．已知向量

  a

  =

  （

  1

  ，

  m

  ）

  ，

  b

  =

  （

  -

  1

  ，

  0

  ）

  ，且

  |

  a

  -

  b

  |

  =

  a

  •

  b

  +

  6

  ，则

  |

  a

  |

  =（　　）

  A． 5

  B． 2 3

  C． 22

  D． 2 6
  组卷：403引用：10难度：0.7

  解析

• 4．部分与整体以某种相似的方式呈现称为分形，一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统，分形几何学不仅让人们感悟到科学与艺术的融合，数学与艺术审美的统一，而且还有其深刻的科学方法论意义，如图，由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于一种分形，具体作法是取一个实心三角形，沿三角形的三边中点连线．将它分成4个小三角形，去掉中间的那一个小三角形后，对其余3个小三角形重复上述过程逐次得到各个图形．
  
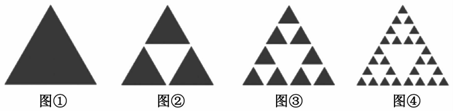
  若记图①三角形的面积为

  3

  4

  ，则第n个图中阴影部分的面积为（　　）

  A． 3 9 • （ 3 2 ） n + 1

  B． 3 6 • （ 3 2 ） n

  C． 3 4 • （ 3 4 ） n

  D． 3 3 • （ 3 4 ） n
  组卷：91引用：7难度：0.7

  解析

• 5．已知矩形ABCD中，AB=2BC，现向矩形ABCD内随机投掷质点P，则满足∠APB为锐角的概率是（　　）

  A． 4 - π 4

  B． π 4

  C． 16 - π 16

  D． π 16
  组卷：114引用：7难度：0.8

  解析

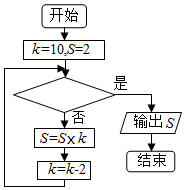• 6．在如图所示的程序框图中，程序运行的结果S为3840，那么判断框中可以填入的关于k的判断条件是（　　）

  A．k＜5

  B．k＞5

  C．k＜4

  D．k＞4
  组卷：39引用：10难度：0.7

  解析

• 7．在2023年成都大运会期间，组委会派遣甲、乙、丙、丁、戍五名志愿者参加A，B，C三个场馆的翻译工作，每人只去1个场馆，每个场馆至少去1人，且甲、乙两人约定去同一个场馆，则不同的派遣方案共有（　　）

  A．24种

  B．36种

  C．48种

  D．64种
  组卷：41引用：2难度：0.7

  解析

（二）选考题：共10分．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分．

• 22．直角坐标系xOy中，点P（0，1），动圆C：（x-sinα）²+（y-3sinα-1）²=1（α∈R）．
  （1）求动圆圆心C的轨迹；
  （2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线M的极坐标方程为：

  ρ

  2

  =

  2

  2

  co

  s

  2

  θ

  +

  si

  n

  2

  θ

  ，过点P的直线l与曲线M交于A，B两点，且

  |

  |

  PA

  |

  -

  |

  PB

  |

  |

  =

  4

  7

  ，求直线l的斜率．
  组卷：109引用：8难度：0.6

  解析

• 23．已知函数f（x）=|2x+3|+|2x-2|，g（x）=sin2x.
  （1）求函数f（x）+g（x）的最小值；
  （2）设a,b∈（-1，1），求证：|2a+1|-|1-2b|＜|2ab+2|．
  组卷：15引用：11难度：0.5

  解析