2023-2024学年贵州省六盘水市高二（上）月考数学试卷（10月份）

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={x∈R|x≤0}，B={x∈R|-1≤x≤1}，则∁_R（A∪B）=（　　）

  A．（-∞，0）

  B．[-1，0]

  C．[0，1]

  D．（1，+∞）
  组卷：168引用：4难度：0.9

  解析

• 2．以

  -

  2

  +

  7

  i

  的虚部为实部，以

  7

  i

  +

  5

  i

  2

  的实部为虚部的复数是（　　）

  A．7-5i

  B． - 2 + 7 i

  C．5+i

  D． 2 + 7 i
  组卷：10引用：2难度：0.7

  解析

• 3．已知向量

  a

  =（1，1，0），则与

  a

  同向共线的单位向量

  e

  =（　　）

  A．（ - 2 2 ， 2 2 ，0）

  B．（0，1，0）

  C．（ 2 2 ， 2 2 ，0）

  D．（-1，-1，0）
  组卷：385引用：16难度：0.9

  解析

• 4．在一次抛硬币的试验中，某同学用一枚质地均匀的硬币做了800次试验，发现正面朝上出现了440次，那么出现正面朝上的频率和概率分别为（　　）

  A．0.55，0.55

  B．0.55，0.5

  C．0.5，0.5

  D．0.5，0.55
  组卷：246引用：6难度：0.7

  解析

• 5．已知空间向量

  a

  ，

  b

  ，

  c

  不共面，且

  2

  a

  +

  b

  -

  c

  =

  （

  z

  -

  1

  ）

  a

  +

  x

  b

  +

  2

  y

  c

  ，则x,y,z的值分别是（　　）

  A．2，1，2

  B．2，1，-2

  C．1， - 1 2 ， 3

  D．1， 1 2 ，3
  组卷：39引用：1难度：0.7

  解析

• 6．已知A（1，1，0），B（0，3，0），C（2，2，3），则向量

  AC

  在

  AB

  上的投影向量的坐标是（　　）

  A． （ - 1 5 ， 2 5 ， 0 ）	B． （ - 1 5 ， 2 5 ， 1 ）
  C． （ - 1 5 ，- 2 5 ， 0 ）	D． （ 1 5 ， 2 5 ， 0 ）
  组卷：33引用：1难度：0.8

  解析

• 7．出租车司机从饭店到火车站途中经过六个交通岗，假设他在各交通岗遇到红灯这一事件是相互独立的，并且概率都是

  1

  3

  ，则这位司机遇到红灯前，已经通过了两个交通岗的概率为（　　）

  A． 1 24

  B． 4 27

  C． 7 9

  D． 1 27
  组卷：59引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出必要的文字说明、证明过程及演算步骤。

• 21．在锐角△ABC中，内角A、B、C所对的边分别为a、b、c,已知a-4cosC=ccosB．
  （1）求b的值；
  （2）若a²+b²+c²=2

  3

  absinC，求△ABC的面积．
  组卷：318引用：5难度：0.5

  解析

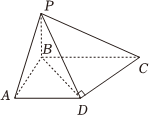• 22．如图，在四棱锥P-ABCD中，已知PB⊥底面ABCD，BC⊥AB，AD∥BC，AB=AD=2．CD⊥PD，异面直线PA和CD所成角等于60°．
  （1）求直线CD和平面PAD所成角的正弦值；
  （2）在棱PA上是否存在一点E，使得平面PAB与平面BDE夹角的正切值为

  5

  ？若存在，指出点E在棱PA上的位置；若不存在，说明理由．
  组卷：15引用：1难度：0.4

  解析