2022-2023学年福建省泉州九中八年级（上）期中数学试卷

一、选择题（本题共10小题，每小题4分，共40分）

• 1．9的算术平方根是（　　）

  A．3

  B．-3

  C．±3

  D． ± 3
  组卷：1621引用：30难度：0.8

  解析

• 2．下列各数中是无理数的是（　　）

  A．3.14

  B． 4

  C． 3

  D． 22 7
  组卷：59引用：4难度：0.9

  解析

• 3．下列运算正确的是（　　）

  A．4a2-2a2=2

  B．（a2）3=a6

  C．a2a3=a6

  D．a3+a2=a5
  组卷：90引用：5难度：0.9

  解析

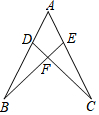• 4．如图所示，AB=AC，要说明△ADC≌△AEB，需添加的条件不能是（　　）

  A．∠B=∠C

  B．AD=AE

  C．∠ADC=∠AEB

  D．DC=BE
  组卷：880引用：93难度：0.9

  解析

• 5．下列选项中，可以用来说明命题“两个锐角的和是锐角”是假命题的反例是（　　）

  A．两个角分别为13°，45°	B．两个角分别为40°，45°
  C．两个角分别为45°，45°	D．两个角分别为105°，45°
  组卷：195引用：10难度：0.7

  解析

• 6．已知x²+kx+16可以用完全平方公式进行因式分解，则k的值为（　　）

  A．-8

  B．±4

  C．8

  D．±8
  组卷：694引用：9难度：0.7

  解析

• 7．估算

  19

  +2的值是在（　　）

  A．5和6之间

  B．6和7之间

  C．7和8之间

  D．8和9之间
  组卷：710引用：106难度：0.9

  解析

• 8．下列各式能用平方差公式进行计算的是（　　）

  A．（x-3）（-x+3）	B．（a+2b）（2a-b）
  C．（a-1）（-a-1）	D．（x-3）2
  组卷：453引用：24难度：0.9

  解析

三、解答题（本题共9小题，共86分）

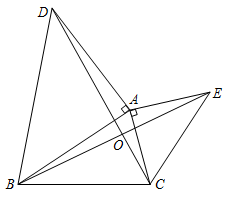• 24．如图，已知以△ABC的边AB、AC分别向外作等腰Rt△ABD与等腰Rt△ACE，其中∠BAD=∠CAE=90°，连接BE、CD，BE和CD相交于点O．
  （1）求证：BE=DC；
  （2）求∠BOC的大小；
  （3）连接DE，取DE的中点F，再连接AF，猜想AF与BC的关系，并证明．
  组卷：411引用：5难度：0.3

  解析

• 25．教科书中这样写道：“我们把多项式a²+2ab+b²及a²-2ab+b²叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．
  例如：分解因式x²+2x-3=（x²+2x+1）-4=（x+1）²-4=（x+1+2）（x+1-2）=（x+3）（x-1）；
  例如求代数式2x²+4x-6的最小值．
  原式=2（x²+2x-3）=2（x+1）²-8．
  可知当x=-1时，2x²+4x-6有最小值，最小值是-8．
  根据阅读材料用配方法解决下列问题：
  （1）用配方法分解因式：x²-4x-5．
  （2）试说明：无论x、y取任何实数时，多项式x²+y²-4x+2y+6的值总为正数．
  （3）当a,b,c分别为△ABC分别为的三边时，且满足a²+b²+c²-6a-6b-10c+43=0时，试判断△ABC的形状并说明理由．
  （4）当a,b为何值时，多项式a²-2ab+2b²-2a-4b+20有最小值，并求出这个最小值．
  组卷：176引用：1难度：0.6

  解析