2022-2023学年黑龙江省哈尔滨九中高二（下）月考数学试卷（6月份）

一、单选题：本题共有8个小题，每小题5分，共40分，在每小题给出的四个选项中是符合题目要求的．

• 1．已知f（x）=xlnx,则曲线y=f（x）在点（1，f（1））处的切线方程为（　　）

  A．x-y-1=0

  B．x-y-2=0

  C．x+y-1=0

  D．x+y-2=0
  组卷：85引用：2难度：0.8

  解析

• 2．对于定义在R上的可导函数f（x），f′（x）为其导函数，下列说法正确的是（　　）

  A．使f'（x）=0的x一定是函数的极值点

  B．f（x）在R上单调递增是f'（x）＞0在R上恒成立的充要条件

  C．若函数f（x）既有极小值又有极大值，则其极小值一定不会比它的极大值大

  D．若f（x）在R上存在极值，则它在R一定不单调
  组卷：60引用：2难度：0.6

  解析

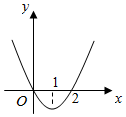• 3．设f'（x）是函数f（x）的导函数，y=f'（x）的图象如图所示，则y=f（x）的图象最有可能的是（　　）

  A．

  B．

  C．

  D．
  组卷：1148引用：32难度：0.7

  解析

• 4．函数

  f

  （

  x

  ）

  =

  1

  3

  x

  3

  +

  1

  2

  a

  x

  2

  +

  x

  -

  1

  存在两个极值点，则实数a的取值范围是（　　）

  A．（-∞，-2）∪（2，+∞）	B．（-∞，-2]∪[2，+∞）
  C．（-2，2）	D．[-2，2]
  组卷：45引用：2难度：0.6

  解析

• 5．设点P在曲线

  y

  =

  lnx

  -

  1

  x

  +

  1

  上，点Q在直线y=2x上，则PQ的最小值为（　　）

  A．2

  B．1

  C． 6 5

  D． 2 5 5
  组卷：235引用：3难度：0.6

  解析

• 6．定义在R上的可导函数f（x）的导函数为f′（x），满足f′（x）＞f（x），f（0）=1，则不等式f（x）＜e^x的解集为（　　）

  A．（-∞，6）

  B．（6，+∞）

  C．（0，+∞）

  D．（-∞，0）
  组卷：44引用：3难度：0.7

  解析

• 7．已知

  a

  =

  ln

  2

  2

  ，

  b

  =

  ln

  3

  6

  ，

  c

  =

  1

  2

  e

  ，则a,b,c的大小为（　　）

  A．b＞c＞a

  B．a＞b＞c

  C．b＞a＞c

  D．c＞b＞a
  组卷：678引用：8难度：0.5

  解析

四、解答题：本题共有6个小题，共70分．

• 21．已知a∈R，函数

  f

  （

  x

  ）

  =

  a

  x

  +

  lnx

  ,

  g

  （

  x

  ）

  =

  ax

  -

  lnx

  -

  2

  ．
  （1）当f（x）与g（x）都存在极小值，且极小值之和为0时，求实数a的值；
  （2）当a=1时，若f（x₁）=f（x₂）=b（x₁≠x₂），求证：x₁+x₂＞2
  组卷：38引用：1难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  klnx

  +

  1

  e

  x

  （

  k

  ∈

  R

  ）

  ．
  （1）若函数y=f（x）在（2，3）上不单调，求k的取值范围；
  （2）已知0＜x₁＜x₂．
  （ⅰ）证明：

  e

  e

  x

  2

  -

  e

  e

  x

  1

  ＞

  -

  ln

  x

  2

  x

  1

  ＞

  1

  -

  x

  2

  x

  1

  ；
  （ⅱ）若

  x

  1

  e

  x

  1

  =

  x

  2

  e

  x

  2

  =

  k

  ，证明：|f（x₁）-f（x₂）|＜1．
  组卷：17引用：1难度：0.5

  解析