2022-2023学年北京市十一学校八年级（上）诊断数学试卷（10月份）
发布：2024/8/24 18:0:9
一、选择题（本题共24分，每小题3分）第1-8题均有四个选项，符合题意的选项只有一个.
-
1．第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（ ）
组卷：1530引用：70难度：0.7 -
2．三角形中，到三个顶点距离相等的点是（ ）
组卷：647引用：8难度：0.8 -
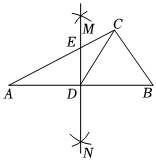3．如图，在△ABC中，分别以点A和点B为圆心，以相同的长（大于）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．已知△CDE的面积比△CDB的面积小4，则△ADE的面积为（ ）12AB组卷：90引用：1难度：0.7 -
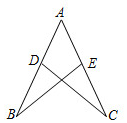4．如图，AB=AC，点D，E分别在AB，AC上，补充下列一个条件后，不能判断△ABE≌△ACD的是（ ）组卷：2214引用：30难度：0.5 -
5．如图，经过直线AB外一点C作这条直线的垂线，作法如下：
（1）任意取一点K，使点K和点C在AB的两旁．
（2）以点C为圆心，CK长为半径作弧，交AB于点D和E．
（3）分别以点D和点E为圆心，大于DE的长为半径作弧，两弧相交于点F．12
（4）作直线CF．则直线CF就是所求作的垂线．根据以上尺规作图过程，若将这些点作为三角形的顶点，其中不一定是等腰三角形的为（ ）组卷：1248引用：26难度：0.7 -
6．“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动、C点固定，OC=CD=DE，点D、E可在槽中滑动．若∠BDE=78°，则∠CDE的度数是（ ）
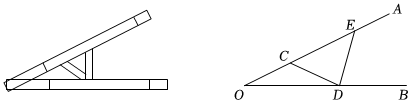组卷：431引用：5难度：0.6 -
7．如图，△ABC是等边三角形，直线l过顶点B，作点C关于直线l的对称点D，连接BD，AD，CD，若∠BAD=25°，则∠BCD的度数为（ ）组卷：151引用：5难度：0.7 -
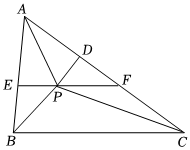8．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点P，过点P作EF∥BC交AB于点E，交AC于点F，过点P作PD⊥AC于点D，下列四个结论中正确的结论有（ ）
①EF=BE+CF；
②∠BPC=180°-∠A；
③点P到△ABC各边的距离相等；
④设PD=m,AE+AF=n,则．S△AEF=12mn组卷：72引用：2难度：0.5
三、解答题（本题共46分，19题、20题、21题各7分：22题、24题每题8分；23题9分）解答应写出文字说明、演算步骤或证明过程.
-
23．（1）操作实践：△ABC中，∠A=90°，∠B=22.5°，请画出一条直线把△ABC分割成两个等腰三角形，并标出分割成两个等腰三角形底角的度数；（要求用两种不同的分割方法）
（2）分类探究：△ABC中，最小内角∠B=28°，若△ABC被一直线分割成两个等腰三角形，请画出相应示意图并写出△ABC最大内角的所有可能值；（以下为备用图）
（3）猜想发现：若一个三角形能被一直线分割成两个等腰三角形，需满足什么条件？（请你至少写出两种不同情况的条件，无需证明）组卷：114引用：2难度：0.3 -
24．如图，在等边△ABC中，点D是线段BC上一点．作射线AD，点B关于射线AD的对称点为E．连接CE并延长，交射线AD于点F．
（1）根据题意，补全图形；
（2）设∠BAF=α，求∠BCF的度数（用α表示）；
（3）用等式表示线段AF、CF、EF之间的数量关系，并证明．
组卷：90引用：3难度：0.3
