2022-2023学年山东省淄博市临淄区八年级（上）期中数学试卷（五四学制）

一、选择题（本题共10小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填在下面的表中，每小题4分，满分40分，错选，不选或选出的答案超过一个，均记0分。）

• 1．式子

  1

  x

  -

  2

  有意义，则x满足的条件是（　　）

  A．x≠0

  B．x＞0

  C．x＞2

  D．x≠2
  组卷：291引用：5难度：0.7

  解析

• 2．下列变形：①x（x-2y）=x²-2xy,②x²+2xy+y²=x²+y（2x+y），③x²-9=（x+3）（x-3），④x²y=x•x•y,其中是因式分解的有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：634引用：4难度：0.9

  解析

• 3．在演讲比赛活动中，7位评委分别给出某位选手的原始评分，评定该选手成绩时，从7个原始评分中去掉一个最高分和一个最低分，得到5个有效评分．5个有效评分与7个原始评分相比，这两组数据不可能变化的是（　　）

  A．中位数

  B．众数

  C．平均数

  D．方差
  组卷：534引用：8难度：0.7

  解析

• 4．若4x²-（k-1）x+9能用完全平方公式因式分解，则k的值是（　　）

  A．13

  B．13或-11

  C．-11

  D．无法确定
  组卷：1348引用：7难度：0.8

  解析

• 5．如果m为整数，那么使分式

  m

  +

  3

  m

  +

  1

  的值为整数的m的值有（　　）

  A．2个

  B．3个

  C．4个

  D．5个
  组卷：2166引用：16难度：0.7

  解析

• 6．已知a,b,c为△ABC的三边，且满足a⁴-b⁴=a²c²-b²c²，则△ABC是（　　）

  A．直角三角形	B．等腰或直角三角形
  C．等腰三角形	D．等腰直角三角形
  组卷：1035引用：5难度：0.6

  解析

• 7．如果把分式

  x

  2

  +

  y

  2

  2

  xy

  中的x,y都扩大3倍，那么分式的值（　　）

  A．扩大3倍

  B．不变

  C．缩小3倍

  D．扩大9倍
  组卷：162引用：5难度：0.7

  解析

三、解答题（第16，17，18，19题每题10分；第20，21题每题12分，第22，23题每题13分；满分90分）解答要写出必要的文字说明、证明过程或演算步骤。

• 22．仔细观察下面的变形规律：

  1

  1

  ×

  2

  =

  1

  1

  -

  1

  2

  ，

  1

  2

  ×

  3

  =

  1

  2

  -

  1

  3

  ，

  1

  3

  ×

  4

  =

  1

  3

  -

  1

  4

  ，……解答下面的问题：
  （1）总结规律：已知n为正整数，请将

  1

  n

  （

  n

  +

  1

  ）

  和

  1

  n

  （

  n

  +

  2

  ）

  写成上面式子的形式；
  （2）类比发现：计算

  1

  1

  ×

  2

  +

  1

  2

  ×

  3

  +

  1

  3

  ×

  4

  +…+

  1

  2021

  ×

  2022

  与

  1

  2

  ×

  4

  +

  1

  4

  ×

  6

  +

  1

  6

  ×

  8

  +…+

  1

  2020

  ×

  2022

  的结果；
  （3）知识迁移：解关于n（n为正整数）的分式方程：

  1

  1

  ×

  3

  +

  1

  3

  ×

  5

  +

  1

  5

  ×

  7

  +…+

  1

  （

  2

  n

  -

  1

  ）

  （

  2

  n

  +

  1

  ）

  =

  n

  +

  100

  2

  n

  +

  202

  ；
  （4）规律应用：化简

  1

  1

  ×

  3

  +

  1

  2

  ×

  4

  +

  1

  3

  ×

  5

  +

  1

  4

  ×

  6

  +…+

  1

  n

  （

  n

  +

  2

  ）

  ．
  组卷：166引用：2难度：0.5

  解析

• 23．【知识再现】在研究平方差公式时，我们在边长为a的正方形中剪掉一个边长为b的小正方形（a＞b），如图1，把余下的阴影部分再剪拼成一个长方形（如图2），根据图1、图2阴影部分的面积关系，可以得到一个关于a,b的等式①

  ．
  【知识迁移】在棱长为a的正方体上挖去一个棱长为b（a＞b）的小正方体后，余下的部分（如图3）再切割拼成一个几何体（如图4）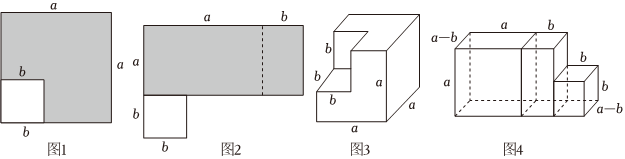
  
  图3中的几何体的体积为②

  ．
  图4中几何体的体积为③

  ．
  根据它们的体积关系得到关于a,b的等式为④

  ．（结果写成整式的积的形式）
  请按照要求在横线处填上合适的式子．
  【知识运用】
  （1）因式分解：8x³-1；
  （2）已知a-b=4，ab=3，求a³-b³的值．
  （3）有人进行了这样的化简

  3

  3

  +

  1

  3

  3

  3

  +

  2

  3

  =

  3

  +

  1

  3

  +

  2

  ，

  5

  3

  +

  2

  3

  5

  3

  +

  3

  3

  =

  5

  +

  2

  5

  +

  3

  ，…面对这样荒谬的约分，一笑之后，再认真检测，发现其结果竟然是正确的！仔细观察式子，我们猜想：

  a

  3

  +

  b

  3

  a

  3

  +

  （

  a

  -

  b

  ）

  3

  =

  a

  +

  b

  a

  +

  （

  a

  -

  b

  ）

  ，试说明此猜想的正确性．（参考公式：x³+y³=（x+y）（x²-xy+y²））
  组卷：150引用：2难度：0.5

  解析