【知识再现】在研究平方差公式时,我们在边长为a的正方形中剪掉一个边长为b的小正方形(a>b),如图1,把余下的阴影部分再剪拼成一个长方形(如图2),根据图1、图2阴影部分的面积关系,可以得到一个关于a,b的等式①a2-b2=(a+b)(a-b)a2-b2=(a+b)(a-b).
【知识迁移】在棱长为a的正方体上挖去一个棱长为b(a>b)的小正方体后,余下的部分(如图3)再切割拼成一个几何体(如图4)
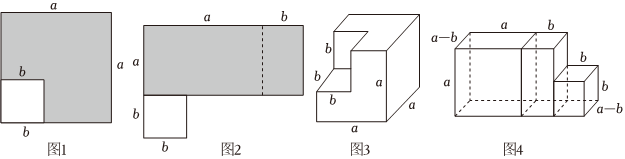
图3中的几何体的体积为②a3-b3a3-b3.
图4中几何体的体积为③a2(a-b)+ab(a-b)+b2(a-b)a2(a-b)+ab(a-b)+b2(a-b).
根据它们的体积关系得到关于a,b的等式为④a3-b3=(a-b)(a2+ab+b2)a3-b3=(a-b)(a2+ab+b2).(结果写成整式的积的形式)
请按照要求在横线处填上合适的式子.
【知识运用】
(1)因式分解:8x3-1;
(2)已知a-b=4,ab=3,求a3-b3的值.
(3)有人进行了这样的化简33+1333+23=3+13+2,53+2353+33=5+25+3,…面对这样荒谬的约分,一笑之后,再认真检测,发现其结果竟然是正确的!仔细观察式子,我们猜想:a3+b3a3+(a-b)3=a+ba+(a-b),试说明此猜想的正确性.(参考公式:x3+y3=(x+y)(x2-xy+y2))
3
3
+
1
3
3
3
+
2
3
=
3
+
1
3
+
2
5
3
+
2
3
5
3
+
3
3
=
5
+
2
5
+
3
a
3
+
b
3
a
3
+
(
a
-
b
)
3
=
a
+
b
a
+
(
a
-
b
)
【答案】a2-b2=(a+b)(a-b);a3-b3;a2(a-b)+ab(a-b)+b2(a-b);a3-b3=(a-b)(a2+ab+b2)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/2 15:0:8组卷:150引用:2难度:0.5
相似题
-
1.阅读材料:利用公式法,可以将一些形如ax2+bx+c(a≠0)的多项式变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c(a≠0)的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解.
例如:.x2+4x-5=x2+4x+(42)2-(42)2-5=(x+42)2-4-5=(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1)
根据以上材料,解答下列问题.
(1)分解因式:x2+2x-3;
(2)求多项式x2+6x-9的最小值;
(3)已知a,b,c是△ABC的三边长,且满足a2+b2+c2+50=6a+8b+10c,求△ABC的周长.发布:2025/6/8 15:30:1组卷:2750引用:10难度:0.3 -
2.已知a+2b=2,ab=3,则2a2b+4ab2=.
发布:2025/6/8 17:0:2组卷:228引用:4难度:0.7 -
3.数形结合思想是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想.我们常利用数形结合思想,借助形的几何直观性来阐明数之间某种关系,如:探索整式乘法的一些法则和公式.
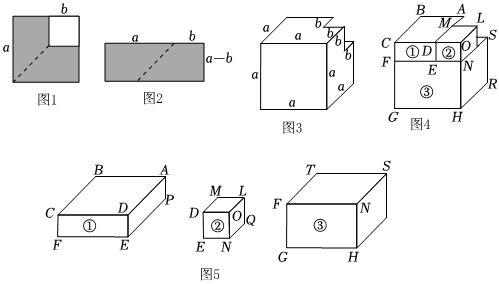
(1)探究一:
将图1的阴影部分沿虚线剪开后,拼成图2的形状,拼图前后图形的面积不变,因此可得一个多项式的分解因式 .
(2)探究二:类似地,我们可以借助一个棱长为a的大正方体进行以下探索:
在大正方体一角截去一个棱长为b(b<a)的小正方体,如图3所示,则得到的几何体的体积为 ;
(3)将图3中的几何体分割成三个长方体①、②、③,如图4、图5所示,∵BC=a,AB=a-b,CF=b,∴长方体①的体积为ab(a-b).类似地,长方体②的体积为 ,长方体③的体积为 ;(结果不需要化简)
(4)用不同的方法表示图3中几何体的体积,可以得到的恒等式(将一个多项式因式分解)为 .
(5)问题应用:利用上面的结论,解决问题:已知a-b=6,ab=2,求a3-b3的值.
(6)类比以上探究,尝试因式分解:a3+b3=.发布:2025/6/8 15:0:1组卷:433引用:4难度:0.6


