当前位置：试卷中心 > 试卷详情

2023-2024学年北京市顺义一中高二（上）月考数学试卷（10月份）

发布：2024/9/2 4:0:8

一.单选题（本大题共10小题，共40.0分）

1．已知向量
a
=（1，2，1），
b
=（-1，0，4），则
a
+2
b
=（　　）
A．（-1，2，9） B．（-1，4，5） C．（1，2，-7） D．（1，4，9）
组卷：438引用：7难度：0.9
解析
2．空间四边形ABCD中，
AB
=
a
，
BC
=
b
，
AD
=
c
，则
CD
等于（　　）
A．
a
+
b
-
c
B．
c
-
a
-
b
C．
a
-
b
-
c
D．
b
-
a
+
c
组卷：248引用：6难度：0.9
解析
3．已知空间向量
a
=（λ，1，-2），
b
=（λ，1，1），则λ=1是
a
⊥
b
的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：98引用：4难度：0.9
解析
4．已知向量
a
=（-1，2，1），
b
=（3，x,y），且
a
∥
b
，那么|
b
|=（　　）
A．
3
6
B．6 C．9 D．18
组卷：433引用：24难度：0.8
解析
5．已知
{
a
，
b
，
c
}
是空间的一个基底，在下列向量中，与向量
a
+
b
，
a
-
b
一定可以构成空间的另一个基底的是（　　）
A．
a
B．
b
C．
c
D．
2
a
-
3
b
组卷：186引用：3难度：0.8
解析
6．在空间直角坐标系中，点A（2，-1，3）关于平面xOz的对称点为B，则
OA
•
OB
=（　　）
A．-10 B．10 C．-12 D．12
组卷：691引用：15难度：0.8
解析
7．已知两点A（-3，4），B（3，2），过点P（1，0）的直线l与线段AB有公共点，则直线l的斜率k的取值范围是（　　）
A．（-1，1） B．（-∞，-1）∪（1，+∞）
C．[-1，1] D．（-∞，-1]∪[1，+∞）
组卷：2091引用：23难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共6小题，共85.0分。解答应写出文字说明，证明过程或演算步骤）

20．如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D、E分别为AC、AB上的点，且DE∥A₁BE，DE=2，将△ADE沿DE折起到△A₁DE的位置，使A₁C⊥CD，如图2．
（1）求证：A₁C⊥平面BCDE；
（2）若M是A₁D的中点，求CM与A₁BE平面所成角的大小；
（3）线段BC上是否存在点P，使平面A₁DP与平面A₁BE垂直？说明理由．
组卷：186引用：2难度：0.5
解析
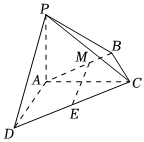21．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BCA=60°，AP=AC=AD=2，E为CD的中点，M在AB上，且
AM
=2
MB
．
（Ⅰ）求证：EM∥平面PAD；
（Ⅱ）求平面PAD与平面PBC所成锐二面角的余弦值；
（Ⅲ）点F是线段PD上异于两端点的任意一点，若满足异面直线EF与AC所成角45°，求AF的长．
组卷：954引用：10难度：0.3
解析