2023年辽宁省阜新市太平区中考数学二模试卷

一、选择题（在每小题给出的四个选项中，只有一个是正确的.每小题3分，共30分）

• 1．在0，-2，4，-4.5这四个数中，绝对值最小的数是（　　）

  A．0

  B．-2

  C．4

  D．-4.5
  组卷：100引用：3难度：0.9

  解析

• 2．如图是由6个完全相同的小正方体组成的几何体，其俯视图为（　　）

  A．

  B．

  C．

  D．
  组卷：3009引用：41难度：0.8

  解析

• 3．在某次体育测试中，九年级一班女同学的一分钟仰卧起坐成绩（单位：个）如下表：
  

  成绩	45	46	47	48	49	50
  人数	1	2	4	2	5	1

  这次测试成绩的中位数和众数分别为（　　）

  A．47，49

  B．47.5，49

  C．48，49

  D．48，50
  组卷：1119引用：20难度：0.9

  解析

• 4．将不等式组

  x + 2 ≥ 0

  2 - x ＞ 0

  的解集在数轴上表示，正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：48引用：7难度：0.9

  解析

• 5．若点A（x₁，-1），B（x₂，2），C（x₃，3）都在反比例函数y=

  6

  x

  的图象上，则x₁，x₂，x₃的大小关系是（　　）

  A．x1＜x2＜x3

  B．x1＜x3＜x2

  C．x2＜x3＜x1

  D．x3＜x1＜x2
  组卷：833引用：8难度：0.6

  解析

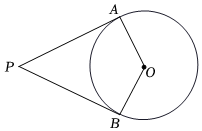• 6．如图，PA，PB是⊙O的切线，A、B为切点，若∠AOB=128°，则∠P的度数为（　　）

  A．32°

  B．52°

  C．64°

  D．72°
  组卷：1873引用：15难度：0.6

  解析

• 7．如图，在一块正三角形飞镖游戏板上画一个正六边形（图中阴影部分），假设飞镖投中游戏板上的每一点是等可能的（若投中边界或没有投中游戏板，则重投1次），任意投掷飞镖1次，则飞镖投中阴影部分的概率为（　　）

  A． 1 3

  B． 4 9

  C． 1 2

  D． 2 3
  组卷：444引用：6难度：0.6

  解析

三、解答题（17、18题每题6分，19、20题每题θ分，21、22题每题

• 22．如图（1），∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
  （1）如图（1），当α=90°时，DE，DF，AD之间满足的数量关系是

  ；
  （2）如图（2），将图（1）中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=

  1

  2

  AD，请给出证明；
  （3）在（2）的条件下，若旋转过程中∠QPN的边PQ与AD的延长线交于点E，其他条件不变，请你探究：在运动变化过程中，（2）中的结论还成立吗？如成立，请说明理由．如不成立，请写出DE，DF，AD之间满足的数量关系，并加以证明．
  
  组卷：223引用：2难度：0.1

  解析

• 23．如图，在平面直角坐标系中，抛物线y=ax²+bx-3（a＞0）与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C．
  （1）求抛物线的解析式；
  （2）点P为直线BC下方抛物线上的一动点，PM⊥BC于点M，PN∥y轴交BC于点N．求线段PM的最大值和此时点P的坐标；
  （3）点E为x轴上一动点，点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，请直接写出点E的坐标；若不存在，请说明理由．
  
  组卷：3811引用：12难度：0.1

  解析