2023年重庆市南开中学高考数学二模试卷

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知全集U={-1，0，1，2，3}，集合A={-1，0，2}，B={0，1}，则（∁_UA）∩（∁_UB）=（　　）

  A．{2}

  B．{3}

  C．{-1，1，2，3}

  D．{-1，0，1，2}
  组卷：293引用：4难度：0.7

  解析

• 2．已知a,b∈R，则“a=b=0”是“ab=0”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：285引用：4难度：0.9

  解析

• 3．已知函数f（x）=ln|x|-e^x，则f（x）的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：373引用：3难度：0.7

  解析

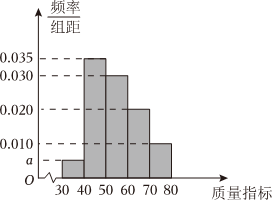• 4．某车间从生产的一批零件中随机抽取了1000个进行一项质量指标的检测，整理检测结果得到此项质量指标的频率分布直方图如图所示．若用分层抽样的方法从质量指标在区间[40，70）的零件中抽取170个进行再次检测，则质量指标在区间[50，60）内的零件应抽取（　　）

  A．30个

  B．40个

  C．60个

  D．70个
  组卷：365引用：3难度：0.7

  解析

• 5．已知a=2^0.2，b=1-2lg2，c=2-log₃10，则a,b,c的大小关系是（　　）

  A．b＞c＞a

  B．a＞b＞c

  C．a＞c＞b

  D．b＞a＞c
  组卷：542引用：3难度：0.7

  解析

• 6．如图，某种中药胶囊外形是由两个半球和一个圆柱组成的，半球的直径是6mm,圆柱高8mm,则该中药胶囊的体积为（　　）

  A．90πmm3

  B．108πmm3

  C．216πmm3

  D．360πmm3
  组卷：397引用：4难度：0.7

  解析

三、解答题：（本大题共5个小题，共75分.解答应写出文字说明，证明过程或演算步骤）

• 19．已知椭圆

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  3

  2

  ，左、右顶点分别为A，B，上顶点为D，坐标原点O到直线AD的距离为

  2

  5

  5

  ．
  （1）求椭圆的方程；
  （2）过A点作两条互相垂直的直线AP，AQ与椭圆交于P，Q两点，求△BPQ面积的最大值．
  组卷：780引用：4难度：0.3

  解析

• 20．已知函数f（x）=xlnx-x+1，g（x）=mlnx+e^-x（m∈R）．
  （1）求f（x）的最小值；
  （2）若0＜a＜1，且

  b

  e

  1

  -

  a

  a

  =

  1

  ，求证：log_ab＞1；
  （3）若g（x）有两个极值点x₁，x₂，证明：|g（x₁）-g（x₂）|＜1．
  组卷：349引用：4难度：0.2

  解析