2023-2024学年广西贵百河三市高二(上)月考数学试卷(10月份)
发布:2024/9/22 6:0:8
一、单选题:共8小题,每小题5分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x|2≤x<4},集合B={x|x2-3x+2<0},则A∪B=( )
组卷:238引用:8难度:0.8 -
2.已知复数
,则|z|=( )z=3+i1+i组卷:35引用:3难度:0.7 -
3.已知
,b=log25,c=log37,则a,b,c的大小顺序是( )a=(53)-12组卷:206引用:5难度:0.7 -
4.已知直线l1:(a-2)x+ay+2=0,l2:x+(a-2)y+a=0,则“l1⊥l2”是“a=-1”的( )
组卷:292引用:7难度:0.8 -
5.已知
,|a|=4,|b|=3,则向量a•b=-6在b方向上的投影向量为( )a组卷:271引用:7难度:0.7 -
6.已知点A(2,2),B(-1,3),若直线kx-y-1=0与线段AB有交点,则实数k的取值范围是( )
组卷:1242引用:12难度:0.7 -
7.已知
,则sin(α+π3)=13=( )cos(2α-π3)组卷:431引用:6难度:0.8
四、解答题:本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
-
21.每年的3月14日为国际数学日,为庆祝该节日,某中学举办了数学文化节,其中一项活动是“数学知识竞赛”,竞赛共分为两轮,每位参赛学生均须参加两轮比赛,若其在两轮竞赛中均胜出,则视为优秀,已知在第一轮竞赛中,学生甲、乙胜出的概率分别为
,45;在第二轮竞赛中,甲、乙胜出的概率分别为p,q.甲、乙两人在每轮竞赛中是否胜出互不影响.35
(1)若,求甲恰好胜出一轮的概率;p=58
(2)若甲、乙各胜出一轮的概率为,甲、乙都获得优秀的概率为会950.625
(i)求p,q,的值;
(ii)求甲、乙两人中至少有一人获得优秀的概率.组卷:265引用:3难度:0.5 -
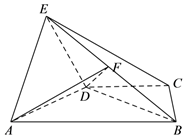 22.已知四棱锥E-ABCD中,四边形ABCD为等腰梯形,AB∥DC,AD=DC=2,AB=4,△ADE为等边三角形,且平面ADE⊥平面ABCD.
22.已知四棱锥E-ABCD中,四边形ABCD为等腰梯形,AB∥DC,AD=DC=2,AB=4,△ADE为等边三角形,且平面ADE⊥平面ABCD.
(1)求证:AE⊥BD;
(2)是否存在一点F,满足(0<λ≤1),且使平面ADF与平面BCE所成的锐二面角的余弦值为EF=λEB.若存在,求出λ的值,否则请说明理由.6513组卷:568引用:9难度:0.4


