2022-2023学年广西柳州地区民族高级中学高一(下)期中数学试卷
发布:2024/7/4 8:0:9
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求)
-
1.复数z=
在复平面内的对应点位于复平面的( )3+4i1-2i组卷:150引用:4难度:0.8 -
2.已知向量
,a=(-1,4),若b=(3,-2λ),则λ=( )a∥(2a+b)组卷:337引用:8难度:0.7 -
3.在△ABC中,角A,B,C的对边分别为a,b,c,若
,则B=( )a=22,b=2,A=π4组卷:266引用:7难度:0.8 -
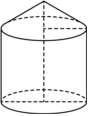 4.如图所示,圆柱与圆锥的组合体,已知圆锥部分的高为,圆柱部分的高为2,底面圆的半径为1,则该组合体的体积为( )12组卷:192引用:5难度:0.7
4.如图所示,圆柱与圆锥的组合体,已知圆锥部分的高为,圆柱部分的高为2,底面圆的半径为1,则该组合体的体积为( )12组卷:192引用:5难度:0.7 -
 5.在平行四边形ABCD中,,则AF=2FC=( )DF组卷:195引用:3难度:0.8
5.在平行四边形ABCD中,,则AF=2FC=( )DF组卷:195引用:3难度:0.8 -
 6.如图,在正方体ABCD-A1B1C1D1中,M,N,P,Q分别为DD1,AD,C1D1,C1C的中点,则异面直线MN与PQ所成的角大小等于( )组卷:212引用:5难度:0.4
6.如图,在正方体ABCD-A1B1C1D1中,M,N,P,Q分别为DD1,AD,C1D1,C1C的中点,则异面直线MN与PQ所成的角大小等于( )组卷:212引用:5难度:0.4 -
7.设△ABC的内角A,B,C所对的边分别为a,b,c,已知sin2B+sin2C-sin2A=sinBsinC,且bcosC+ccosB=2,则△ABC的面积的最大值为( )
组卷:460引用:6难度:0.5
四、解答题(共70分,解答应写出文字说明,证明过程或演算步骤)
-
21.设△ABC的内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为
,且332.cosBcosC=b2a-c
(1)求角B;
(2)若,求BM的最小值.AM=2MC组卷:49引用:2难度:0.5 -
 22.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥BC,PA=AD=4,BC=1,,AB=3.CD=23
22.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥BC,PA=AD=4,BC=1,,AB=3.CD=23
(1)证明:DC⊥平面PAC;
(2)求AD与平面PCD所成角的余弦值.组卷:344引用:7难度:0.5


