2022-2023学年山东省淄博市某县七年级（下）期末数学试卷（五四学制）

一、选择题：本大题共10个小题，每小题4分，共40分.在每小题所给出的四个选项中，只有一项是符合题目要求的.

• 1．在下列数学表达式中，不等式的个数是（　　）
  ①-3＜0；
  ②4x+3y＞0；
  ③x=3；
  ④x≠5；
  ⑤x+2＞y+3．

  A．2个

  B．3个

  C．4个

  D．5个
  组卷：171引用：4难度：0.9

  解析

• 2．若a＞b,则下列不等式正确的是（　　）

  A．3a＜3b

  B．ma＞mb

  C．-a-1＞-b-1

  D． a 2 +1＞ b 2 +1
  组卷：1098引用：24难度：0.9

  解析

• 3．随机事件发生的机会是（　　）

  A．100%	B．0
  C．0和1之间的一个数	D．以上都不对
  组卷：70引用：3难度：0.9

  解析

• 4．若不等式（m+2）x＞m+2的解集是x＜1，则m的取值范围是（　　）

  A．m＞2

  B．m＜-2

  C．m＞-2

  D．m＜2
  组卷：391引用：5难度：0.9

  解析

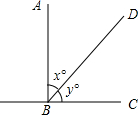• 5．如图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC度数分别为x,y,那么可列方程组为（　　）

  A． x + y = 90 x = y - 15	B． x + y = 90 x = 15 - 2 y
  C． x + y = 90 x = 2 y - 15	D． 2 x = 90 x = 2 y - 15
  组卷：113引用：3难度：0.7

  解析

• 6．已知关于x,y的二元一次方程组

  x + 3 y = 4 - a

  x - y = 3 a

  ，给出下列结论中正确的个数是（　　）
  ①当这个方程组的解x,y的值互为相反数时，a=-2；
  ②当a=1时，方程组的解也是方程 x+y=4+2a 的解；
  ③无论a取什么实数，x+2y的值始终不变．

  A．0

  B．1

  C．2

  D．3
  组卷：138引用：2难度：0.6

  解析

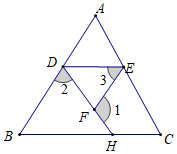• 7．如图，在△ABC中，已知∠1+∠2=180°，∠3=∠B=72°，∠AED=58°，则∠C=（　　）

  A．32°

  B．58°

  C．72°

  D．108°
  组卷：859引用：4难度：0.5

  解析

三、解答题：本大题共8小题，共90分，请写出必要的文字说明、证明过程或演算步骤.

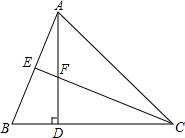• 22．如图，在△ABC中，AD⊥BC于D，CE平分∠ACB分别交AB、AD于E、F两点，且BD=FD，AB=CF．求证：
  （1）CE⊥AB；
  （2）AE=BE．
  组卷：791引用：3难度：0.5

  解析

• 23．如图，已知直线AB∥射线CD，∠CEB=100°．P是射线EB上一动点，过点P作PQ∥EC交射线CD于点Q，连接CP．作∠PCF=∠PCQ，交直线AB于点F，CG平分∠ECF．
  
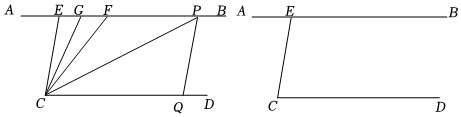
  （1）若点P，F，G都在点E的右侧，求∠PCG的度数；
  （2）若点P，F，G都在点E的右侧，∠EGC-∠ECG=30°，求∠CPQ的度数；
  （3）在点P的运动过程中，是否存在这样的情形，使∠EGC：∠EFC=4：3？若存在，求出∠CPQ的度数；若不存在，请说明理由．
  组卷：484引用：4难度：0.5

  解析