当前位置：试卷中心 > 试卷详情

2022-2023学年广东省深圳市光明区八年级（下）期末数学试卷

发布：2024/6/21 8:0:10

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，其中只有一项是正确的）

1．下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（　　）
A． B． C． D．
组卷：354引用：12难度：0.9
解析
2．要使分式
8
a
+
3
有意义，a应满足的条件是（　　）
A．a＜-3 B．a＞-3 C．a=-3 D．a≠-3
组卷：576引用：3难度：0.7
解析
3．如图，在▱ABCD中，∠A=140°，则∠D的度数为（　　）
A．40° B．70° C．110° D．140°
组卷：319引用：1难度：0.7
解析
4．若a＞b,则下列结论不成立的是（　　）
A．2a＞2b B．
a
2
＞
b
2
C．a+m＞b+m D．-4a＞-4b
组卷：438引用：4难度：0.7
解析
5．下列各式从左到右的变形属于因式分解的是（　　）
A．x（a+b）=ax+bx
B．a²+4a+4=（a+2）（a-2）
C．10a²+5a=5a（2a+1）
D．a²-16+3a=（a+4）（a-4）+3a
组卷：629引用：2难度：0.9
解析
6．点M（3，-1）先向左平移3个单位长度，再向上平移2个单位长度得到的点的坐标是（　　）
A．（0，-3） B．（0，1） C．（6，-3） D．（6，1）
组卷：297引用：2难度：0.6
解析
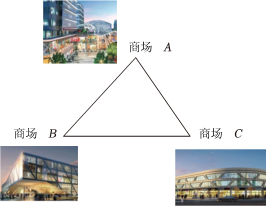7．如图，三座商场分别坐落在A、B、C所在位置，现要规划一个地铁站，使得该地铁站到三座商场的距离相等，该地铁站应建在（　　）
A．三角形三条中线的交点
B．三角形三条高所在直线的交点
C．三角形三个内角的角平分线的交点
D．三角形三条边的垂直平分线的交点
组卷：517引用：8难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共7小题，共55分）

21．如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，在建立平面直角坐标系后，点C的坐标为（-2，-1）．

（1）将△ABC向上平移6个单位得到△A₁B₁C₁，画出△A₁B₁C₁；
（2）以（0，-1）为对称中心，画出△ABC关于该点对称的△A₂B₂C₂；
（3）经探究发现，△A₁B₁C₁和△A₂B₂C₂成中心对称，则对称中心坐标为
；
（4）已知点P为x轴上不同于O、D的动点，当PA+PC=
时，∠OPC=∠DPA．
组卷：702引用：3难度：0.5
解析
22．问题情境：在学习《图形的平移和旋转》时，数学兴趣小组遇到这样一个问题：如图1，点D为等边△ABC的边BC上一点，将线段AD绕点A逆时针旋转60°得到线段AE，连接CE．

（1）【猜想证明】试猜想BD与CE的数量关系，并加以证明；
（2）【探究应用】如图2，点D为等边△ABC内一点，将线段AD绕点A逆时针旋转60°得到线段AE，连接CE，若B、D、E三点共线，求证：EB平分∠AEC；
（3）【拓展提升】如图3，若△ABC是边长为2的等边三角形，点D是线段BC上的动点，将线段AD绕点D顺时针旋转60°得到线段DE，连接CE．点D在运动过程中，△DEC的周长最小值=
（直接写答案）．
组卷：1696引用：5难度：0.1
解析