2022-2023学年四川省成都市武侯区玉林中学高一（下）诊断数学试卷（5月份）

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知z=2-3i（i虚数单位），则z的共轭复数

  z

  的虚部为（　　）

  A．2

  B．i

  C．3

  D．3i
  组卷：41引用：2难度：0.8

  解析

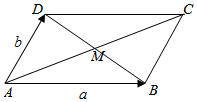• 2．如图，平行四边形ABCD的两条对角线相交于点M，且

  AB

  =

  a

  ，

  AD

  =

  b

  ，则

  MD

  =（　　）

  A． 1 2 a + 1 2 b

  B．- 1 2 a - 1 2 b

  C． 1 2 a - 1 2 b

  D．- 1 2 a + 1 2 b
  组卷：209引用：7难度：0.7

  解析

• 3．在△ABC中，已知a=8，B=60°，C=75°，则b等于（　　）

  A．4 6

  B． 5

  C．4 3

  D． 22 3
  组卷：249引用：28难度：0.9

  解析

• 4．若sin（π-α）=

  3

  5

  ，则cos2α=（　　）

  A．- 24 25

  B．- 7 25

  C． 7 25

  D． 24 25
  组卷：442引用：6难度：0.8

  解析

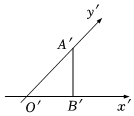• 5．一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′，若O′B′=2，那么原△ABO的面积是（　　）

  A．1

  B． 2

  C． 2 2

  D． 4 2
  组卷：400引用：9难度：0.9

  解析

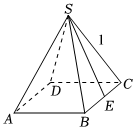• 6．如图所示，侧棱长为1的正四棱锥，若底面周长为4，则这个棱锥的侧面积为（　　）

  A．5

  B． 3

  C． 3 + 1 2

  D． 3 + 1
  组卷：156引用：1难度：0.8

  解析

• 7．若圆锥的表面积为6π，圆锥的高与母线长之比

  3

  ：

  2

  ，则该圆锥的体积为（　　）

  A． 2 6 π 3

  B． 2 6 π

  C． 3 2 π 4

  D． 9 2 π 4
  组卷：170引用：2难度：0.7

  解析

四、解答题：本大题有6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

• 21．在①

  m

  =

  （

  2

  a

  -

  c

  ,

  b

  ）

  ，

  n

  =

  （

  cos

  C

  ，

  cos

  B

  ）

  ，

  m

  ∥

  n

  ；②

  bsin

  A

  =

  acos

  （

  B

  -

  π

  6

  ）

  ；③（a+b）（a-b）=（a-c）c三个条件中任选一个，补充在下面的问题中，并解决该问题．在△ABC中，内角A，B，C的对边分别是a,b,c,且满足____．
  （1）求角B；
  （2）若b=2，求△ABC面积的最大值．
  组卷：91引用：4难度：0.6

  解析

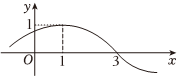• 22．已知函数f（x）=Asin（ωx+φ）

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，

  0

  ＜

  φ

  ＜

  π

  2

  ）

  的部分图象如图所示，最高点的坐标为（1，1）．
  （1）求函数f（x）的解析式；
  （2）若存在

  x

  ∈

  [

  -

  5

  3

  ，

  3

  ]

  ，对任意a∈[-1，1]，不等式

  f

  （

  x

  ）

  -

  m

  2

  +

  2

  am

  +

  7

  2

  ≤

  0

  恒成立，求m的取值范围．
  组卷：71引用：1难度：0.5

  解析