当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省宁波市鄞州区钟公庙中学九年级（上）月考数学试卷（12月份）

发布：2024/8/16 11:0:4

一、选择题（每小题4分，共40分）

1．抛物线y=-（x+2）²-4的对称轴是（　　）
A．直线x=-2 B．直线x=2 C．直线x=-4 D．直线x=4
组卷：86引用：3难度：0.7
解析
2．在Rt△ABC中，∠C=90°，AB=5，BC=3，则tanA的值是（　　）
A．
4
5
B．
4
3
C．
3
5
D．
3
4
组卷：1920引用：11难度：0.7
解析
3．下列语句中，正确的有（　　）
①相等的圆心角所对的弧相等；
②圆内接四边形的对角互补；
③长度相等的两条弧是等弧；
④平分弦的直径垂直于弦，并且平分弦所对的弧．
A．4个 B．3个 C．2个 D．1个
组卷：96引用：3难度：0.6
解析
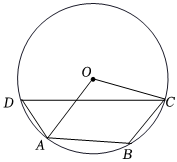4．如图，四边形ABCD是⊙O的内接四边形，∠B=130°，则∠AOC的度数是（　　）
A．100° B．110° C．120° D．130°
组卷：186引用：4难度：0.7
解析
5．已知点（-1，y₁），（-2，y₂），（-4，y₃）在二次函数y=-2x²-8x+c的图象上，则y₁，y₂，y₃的大小关系是（　　）
A．y₁＜y₃＜y₂ B．y₃＜y₂＜y₁ C．y₃＜y₁＜y₂ D．y₂＜y₃＜y₁
组卷：142引用：3难度：0.6
解析
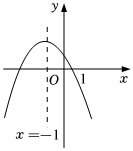6．二次函数y=ax²+bx+c（a≠0）的图象如图，给出下列四个结论：
①abc＜0；②2a-b=0；③4ac-b²＞0；④c-a＞0，其中正确结论的个数是（　　）
A．4个 B．3个 C．2个 D．1个
组卷：227引用：5难度：0.5
解析
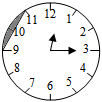7．如图，有一个半径为2的圆形时钟，其中每个相邻刻度间的弧长均相等，过9点和11点的位置作一条线段，则钟面中阴影部分的面积为（　　）
A．
2
3
π-
3
2
B．
2
3
π-
3
C．
4
3
π-2
3
D．
4
3
π-
3
组卷：1905引用：18难度：0.5
解析
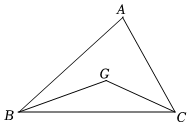8．如图，已知点G是△ABC的重心，那么S_△BCG：S_△ABC等于（　　）
A．1：2 B．1：3 C．2：3 D．2：5
组卷：916引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（第17，18，19题各8分，第20，21，22题各10分，第23题12分，第24题14分）

23．（1）如图1，在矩形ABCD中，AB：BC=3：2，点E、F分别在线段BC、CD上，且AE⊥BF，则
BF
AE
=
；
（2）如图2，在矩形ABCD中，AB：BC=3：2，点F、G分别在边AB、CD上，将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形EFGP，EP交CD于点H，连接AE交GF于点O．试探究GF与AE之间的位置关系与数量关系，并说明理由；
（3）在（2）的条件下，连接CP，若
BE
BF
=
3
4
，
GF
=
2
10
，求线段BE和CP的长．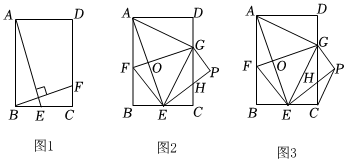
组卷：85引用：3难度：0.2
解析
24．定义：如果一个三角形中有两个内角α，β满足α+2β=90°，那我们称这个三角形为“近直角三角形”．
（1）若△ABC是“近直角三角形”，∠B＞90°，∠C=50°，则∠A=
度；
（2）如图1，在Rt△ABC中，∠BAC=90°，AB=3，AC=4．若BD是∠ABC的平分线，
①求证：△BDC是“近直角三角形”；
②在边AC上是否存在点E（异于点D），使得△BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由．
（3）如图2，在Rt△ABC中，∠BAC=90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连接AE交BD于点F，若△BCD为“近直角三角形”，且AB=5，AF=3，求tan∠C的值．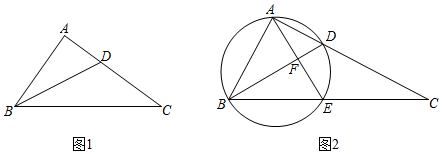
组卷：1910引用：5难度：0.1
解析