2022-2023学年云南省文山州马关一中高三（上）第七次月考数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知全集U=R，A={x|1≤x≤3}，B={x|x＞1}，则A∩（∁_UB）=（　　）

  A．[-3，1]

  B．[1，3]

  C．{1}

  D．（-∞，0]
  组卷：0引用：2难度：0.7

  解析

• 2．已知复数z满足z（2+i）=2-i,其中i为虚数单位，则|z|=（　　）

  A． 1 3

  B． 1 2

  C．1

  D．2
  组卷：83引用：4难度：0.9

  解析

• 3．下列函数中，值域为R且为奇函数的是（　　）

  A． y = 1 x

  B．y=tanx

  C．y=1-x3

  D．y=2x
  组卷：6引用：2难度：0.7

  解析

• 4．等差数列{a_n}中，a₁-2a₂=6，S₃=-27，当S_n取得最小值时，n的值为（　　）

  A．4或5

  B．5或6

  C．4

  D．5
  组卷：11引用：2难度：0.7

  解析

• 5．函数f（x）=cosx+sin2x的图象大致为（　　）

  A．	B．
  C．	D．
  组卷：67引用：3难度：0.9

  解析

• 6．已知正数a,b满足a²+2b²=1，则ab²的最大值是（　　）

  A． 1 3

  B． 3 3

  C． 3 9

  D． 1 9
  组卷：9引用：2难度：0.6

  解析

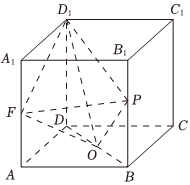• 7．如图所示，在正方体ABCD-A₁B₁C₁D₁中，O，F分别为BD，AA₁的中点，点P为棱BB₁上的动点（不含端点），设二面角F-D₁O-P的平面角为α，直线OF与平面OPD₁所成角为β，则（　　）

  A．α＞β	B．α＜β
  C．α=β	D．以上均有可能
  组卷：25引用：2难度：0.5

  解析

四.解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．已知双曲线C：

  x

  2

  a

  2

  -y²=1的右焦点为F，点M，N分别为双曲线C的左、右顶点，过点F的直线l交双曲线的右支于P，Q两点，设直线MP，NP的斜率分别为k₁，k₂，且k₁k₂=

  1

  3

  ．
  （1）求双曲线C的方程；
  （2）当点P在第一象限，且

  tan

  ∠

  MPN

  tan

  ∠

  MQN

  =

  1

  2

  时，求直线l的方程．
  组卷：242引用：5难度：0.5

  解析

• 22．已知函数f（x）=e^2x-ax²-

  1

  2

  ，

  g

  （

  x

  ）

  =

  2

  x

  2

  （

  e

  x

  -

  x

  2

  +

  x

  ）

  
  （1）若f（x）在R上单调递增，求a的取值范围；
  （2）当a=-1时，证明：f（x）＞g（x）．
  组卷：4引用：2难度：0.2

  解析