2022-2023学年重庆八中九年级（上）期末数学试卷

一、选择题（本大题共12小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，请将答题卡上对应选项的代号涂黑.

• 1．保护环境，人人有责，下列四个图形是生活中常见的垃圾回收标志，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：190引用：11难度：0.9

  解析

• 2．抛物线y=（x-3）²+5的顶点坐标是（　　）

  A．（3，-5）

  B．（-3，5）

  C．（3，5）

  D．（-5，-5）
  组卷：221引用：2难度：0.7

  解析

• 3．计算（2ab）²的正确结果为（　　）

  A．2a2b2

  B．4ab

  C．4a2b2

  D．2ab2
  组卷：560引用：2难度：0.9

  解析

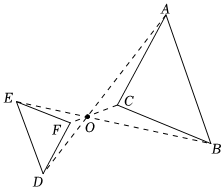• 4．如图，已知△ABC和△DEF位似，位似中心为点O，且

  AO

  DO

  =

  3

  2

  ，若△ABC的周长为9，则△DEF的周长为（　　）

  A．4

  B．6

  C．12

  D．13.5
  组卷：177引用：3难度：0.7

  解析

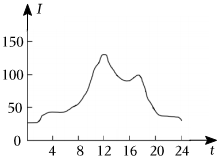• 5．如图所示的曲线表示的是重庆某日空气质量指数I随时间t（单位：h）的变化情况，则当I取得最大值时，对应的t的值大约为（　　）

  A．8

  B．12

  C．16

  D．20
  组卷：153引用：3难度：0.7

  解析

• 6．估计（

  3

  +

  2

  ）×

  2

  的值应在（　　）

  A．1到2之间

  B．2到3之间

  C．3到4之间

  D．4到5之间
  组卷：89引用：3难度：0.6

  解析

• 7．用字母“C”，“H”按如图所示的规律拼图案，其中第①个图案中有4个“H”，第②个图案中有6个“H”，第③个图案中有8个“H”，按此规律排列下去，则第⑥个图案中字母“H”的个数为（　　）
  

  A．11

  B．12

  C．13

  D．14
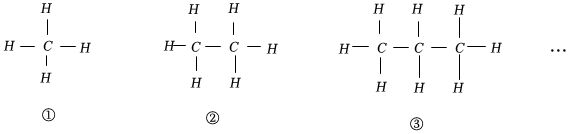  组卷：65引用：2难度：0.6

  解析

• 8．进入12月以来，某大型商场前三周的营业收入持续上涨，若12月第1周营业收入为3亿元，这三周的营业总收入为13亿元，若平均每周的增长率记为x,则方程可以列为（　　）

  A．3（1+x）=13	B．3（1+x）2=13
  C．3+3（1+x）2=13	D．3+3（1+x）+3（1+x）2=13
  组卷：280引用：4难度：0.6

  解析

三、解答题（本大题共9个小题，17、18每小题8分，19-25每小题8分，共86分）解答题时每小题必须给出必要的演算过程或推理步骤，画出必要的图形(包括作辅助线)，请将解答过程书写在答题卡中对应的位置上.

• 24．如图1所示，抛物线y=-

  1

  2

  x

  2

  +x+4与x轴交于A、B两点（点A在点B左侧），与y轴交于C．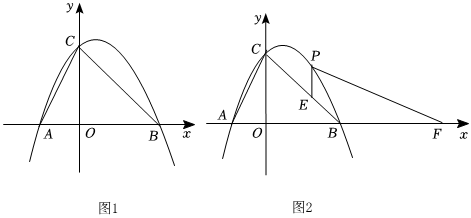
  
  （1）求△ABC的面积；
  （2）如图2所示，点P是直线BC上方抛物线上的动点，过点P作直线PE∥y轴交BC于点E，过点P作直线PF⊥AC交x轴于点F，请求出PE+

  5

  5

  PF的最大值及此时点P的坐标；
  （3）将抛物线y=-

  1

  2

  x

  2

  +x+4向左平移

  7

  2

  个单位，得到新抛物线y'，点M是新抛物线y'对称轴上一点，N为平面直角坐标系内一点，直接写出所有使得以点B、C、M、N为顶点的菱形的点N的坐标，并写出其中一个点N坐标的求解过程．
  组卷：561引用：2难度：0.4

  解析

• 25．在△ABC中，∠ACB=90°，AC=BC，D是AC边上一动点，连接BD．
  
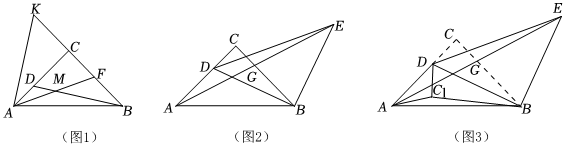
  （1）如图1，在平面内将线段DC绕点C顺时针旋转90°得到线段CK，点F为BC边上一点，连接AF交BD于M，连接AK．若∠CAF=2∠DBA，AF=8，AK=10，求CF的长；
  （2）如图2，在平面内将线段DB绕点B顺时针旋转一定角度得到线段BE，连接AE交BC于G，连接DE，若∠CDE=∠DBA，猜想线段AD，CG的数量关系，并证明你的猜想；
  （3）在（2）的条件下，将△CDB沿BD直线BD翻折至△ABC所在平面内得到△BDC₁，连接AC₁，若AC=2+

  2

  ，在点D运动过程中，当线段AC₁取得最小值时，请直接写出△ABE与四边形BCDC₁重叠部分的面积．
  组卷：569引用：2难度：0.3

  解析