当前位置：试卷中心 > 试卷详情

2022-2023学年江西省吉安三中（艺术类）高一（下）期末数学试卷

发布：2024/6/29 8:0:10

1．已知集合A={1，2，3，4}，B={-1，0，1}，则A∩B=（　　）
A．{0} B．{1} C．{2，3} D．{-1，0，1}
组卷：106引用：3难度：0.7
解析
2．“x＞0”是“x≥3”的（　　）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
组卷：135引用：5难度：0.7
解析
3．220°=（　　）
A．
11
π
36
B．
11
π
18
C．
11
π
9
D．
7
π
6
组卷：244引用：5难度：0.8
解析
4．若sinA=
1
3
，则sin（6π-A）的值为（　　）
A．
1
3
B．
-
1
3
C．
-
2
2
3
D．
2
2
3
组卷：304引用：4难度：0.9
解析
5．已知△ABC的面积为
3
2
，且b=2，
c
=
3
，则A=（　　）
A．30° B．60° C．150° D．120°或60°
组卷：5引用：3难度：0.8
解析
6．已知向量
a
，
b
满足
a
•
b
=
5
，且
b
=
（
3
，-
4
）
，则
a
在
b
上的投影向量为（　　）
A．
（
3
5
，-
4
5
）
B．
（
-
3
5
，
4
5
）
C．（3，-4） D．（-3，4）
组卷：123引用：2难度：0.7
解析
7．函数
f
（
x
）
=
2
sin
（
x
+
5
π
6
）
sin
（
x
+
π
3
）
图象的对称轴可以是（　　）
A．直线
x
=
5
π
12
B．直线
x
=
π
3
C．直线
x
=
π
6
D．直线
x
=
2
π
3
组卷：238引用：8难度：0.7
解析

21．已知函数
f
（
x
）
=
sin
（
ωx
+
π
6
）
+
sin
（
ωx
-
π
6
）
-
2
co
s
2
ωx
2
，
x
∈
R
（其中ω＞0）．
（1）求函数f（x）的值域；
（2）若函数y=f（x）的图象上所有点的横坐标缩短为原来的
1
2
（纵坐标不变）得到函数g（x）的图象，且函数y=g（x）+1的图象与x轴的相邻两交点间的距离为
π
2
，求函数y=g（x）的单调递增区间．
组卷：90引用：3难度：0.5
解析
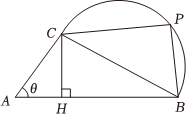22．高邮某公司欲生产一款迎春工艺品回馈消费者，工艺品的平面设计如图所示，该工艺品由直角三角形ABC和以BC为直径的半圆拼接而成，点P为半圆上一点（异于B，C），点H在线段AB上，且满足CH⊥AB．已知∠ACB=90°，AB=10cm,设∠CAB=θ．
（1）为了使工艺礼品达到最佳观赏效果，需满足∠ABC=∠PCB，CA+CP达到最大．当θ为何值时，工艺礼品达到最佳观赏效果；
（2）为了工艺礼品达到最佳稳定性便于收藏，需满足∠PBA=60°，且CH+CP达到最大．当θ为何值时，CH+CP取得最大值，并求该最大值．
组卷：208引用：6难度：0.5
解析