2022-2023学年云南省保山市、文山州高一(下)期末数学试卷
发布:2024/6/24 8:0:9
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的)
-
1.集合A={x|1<x<8},集合B={1,3,5,6,7},则A∩B=( )
组卷:88引用:2难度:0.8 -
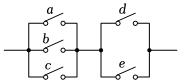 2.有一组电路开关如图所示,现在开关a、b、c、d、e是处于断开状态,任意闭合其中的两个,则电路接通的概率是( )组卷:36引用:2难度:0.7
2.有一组电路开关如图所示,现在开关a、b、c、d、e是处于断开状态,任意闭合其中的两个,则电路接通的概率是( )组卷:36引用:2难度:0.7 -
3.已知m,n是不同的直线,α,β是不同的平面,下列命题中,正确的是( )
组卷:100引用:5难度:0.7 -
4.已知sin2α=
,则cos2(α-14)=( )π4组卷:120引用:2难度:0.8 -
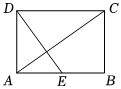 5.如图所示,在矩形ABCD中,AB=2,点E为AB的中点,且,则DE⊥AC等于( )|DE|组卷:154引用:2难度:0.5
5.如图所示,在矩形ABCD中,AB=2,点E为AB的中点,且,则DE⊥AC等于( )|DE|组卷:154引用:2难度:0.5 -
6.已知一组数据1.3,2.1,2.6,3.7,5.5,7.9,x,9.9的第65百分位数是7.9,则实数x的取值范围是( )
组卷:46引用:3难度:0.8 -
7.已知
为增函数,则a的取值范围是( )f(x)=(-a+4)x-3a,x<-1,x2+ax-8,x≥-1,组卷:570引用:3难度:0.8
四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
-
21.已知函数f(x)=loga(1-x)+3,(a>0且a≠1)的图象经过点P(-2,4),函数
为奇函数.g(x)=b-23x+1
(1)求函数f(x)的解析式;
(2)求函数F(x)=g(x)+3x-2的零点;
(3)若关于x的不等式在区间(-1,0)上恒成立,求正实数m的取值范围.m+log3(1+x1-x)<f(x)组卷:29引用:3难度:0.4 -
 22.如图所示,在四棱锥P-ABCD中,该四棱锥的底面ABCD是边长为6的菱形,∠ABC=120°,PA=PC,∠PBD=∠PDB=60°,E为线段AB上靠近B点的三等分点.
22.如图所示,在四棱锥P-ABCD中,该四棱锥的底面ABCD是边长为6的菱形,∠ABC=120°,PA=PC,∠PBD=∠PDB=60°,E为线段AB上靠近B点的三等分点.
(1)证明:平面PAC⊥平面PBD;
(2)在线段PD上是否存在一点F,使得EF∥平面PBC?若存在,求的值及直线EF与平面ABCD所成角的大小;若不存在,请说明理由.PFPD组卷:109引用:4难度:0.6


