2022-2023学年四川省成都市青羊区石室中学高二（下）期中数学试卷（理科）

一、选择题（本题共12道小题，每小题5分，共60分）

• 1．在复平面内，复数z对应的点的坐标是（-2，1），则zi的虚部为（　　）

  A．2i

  B．2

  C．-2i

  D．-2
  组卷：49引用：4难度：0.8

  解析

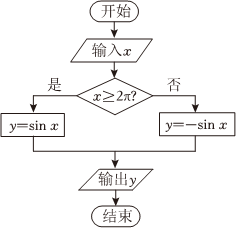• 2．执行如图所示的程序框图，若输入

  x

  =

  7

  π

  3

  ，则输出y的值为（　　）

  A． 3 2

  B． - 3 2

  C． 1 2

  D． - 1 2
  组卷：10引用：5难度：0.8

  解析

• 3．若实数x,y满足约束条件

  x - 2 y ≤ 4

  x - y ≥ 3

  y ≤ 1

  ，则z=x+6y的最小值为（　　）

  A．-6

  B．-5

  C．-4

  D．-3
  组卷：29引用：3难度：0.5

  解析

• 4．德国哲学家、数学家莱布尼茨（GottfriedWilhelmLeibniz）是历史上少见的通才，被誉为十七世纪的亚里士多德，他的一个重要数学发明是二进位制，他本人也确认，中国人在三千多年前的《易经》64卦里就藏匿了这个奥妙．莱布尼茨用数0表示空位，数1表示实位，即满2进1．这样一来，所有的自然数都可以用这两个数来表示了，例如：自然数0为二进位制中的0，自然数1为二进位制中的1，自然数2为二进位制中的10，自然数3为二进位制中的11，自然数4为二进位制中的100，自然数5为二进位制中的101，…．由以上二进位制的规则，可知二进位制中的10101表示的自然数是（　　）

  A．11

  B．21

  C．25

  D．42
  组卷：29引用：3难度：0.8

  解析

• 5．已知f（x）是R上的奇函数，且f（x）=f（2-x），当x∈[0，1]时，f（x）=2^x-1，则f（2024）+f（2023）=（　　）

  A．-1

  B．1

  C．0

  D．2
  组卷：77引用：2难度：0.8

  解析

• 6．a²+b²=1是asinθ+bcosθ≤1恒成立的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：83引用：9难度：0.9

  解析

• 7．已知抛物线x²=4y的焦点为F，准线为l,过抛物线上一点P作l的垂线，垂足为A，若

  FA

  在x轴正方向上的投影为

  2

  3

  ，则△PAF的面积为（　　）

  A． 2 3

  B． 4 3

  C． 3

  D．6
  组卷：82引用：3难度：0.6

  解析

三、解答题（本题共6道小题，17题10分，其余各题12分，共70分）

• 21．已知离心率为

  2

  2

  的椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左焦点为F，左、右顶点分别为A₁、A₂，上顶点为B，且△A₁BF的外接圆半径大小为

  3

  ．
  （1）求椭圆C方程；
  （2）设斜率存在的直线l交椭圆C于P，Q两点（P，Q位于x轴的两侧），记直线A₁P、A₂P、A₂Q、A₁Q的斜率分别为k₁、k₂、k₃、k₄，若

  k

  1

  +

  k

  4

  =

  5

  3

  （

  k

  2

  +

  k

  3

  ）

  ，求△A₂PQ面积的取值范围．
  组卷：187引用：6难度：0.5

  解析

• 22．在平面直角坐标系xOy中，曲线C₁的参数方程为

  x = 3 sinα ，

  y = 2 cosα

  （α为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为

  ρ

  （

  2

  cosθ

  +

  sinθ

  ）

  =

  6

  ，其中ρ＞0，0≤θ＜2π．
  （1）求C₁的普通方程与直线l的直角坐标方程；
  （2）直线l与曲线C₁交于A，B两点，且A，B两点对应的极角分别为θ₁，θ₂，求θ₁+θ₂的值．
  组卷：133引用：9难度：0.5

  解析