当前位置：试卷中心 > 试卷详情

2022-2023学年北京市丰台八中七年级（下）期中数学试卷

发布：2024/7/12 8:0:9

一、选择题（本题共30分，每小题3分）第1-8题均有四个选项，符合题意的选项只有一个.

1．在平面直角坐标系中，点（1，-2）所在的象限是（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：953引用：18难度：0.9
解析
2．9的算术平方根是（　　）
A．±3 B．±
3
C．
3
D．3
组卷：176引用：18难度：0.9
解析
3．下列各数中，无理数是（　　）
A．0.3 B．
1
2
C．
3
D．-
4
组卷：126引用：5难度：0.9
解析
4．如果a＞b,那么下列不等式成立的是（　　）
A．a+2＜b+2 B．-2a＜-2b C．
1
2
a
＜
1
2
b
D．a²＞b²
组卷：586引用：6难度：0.8
解析
5．如图．将含30°角的直角三角板的直角顶点放在直尺的一边上，已知∠1=35°，则∠2的度数是（　　）
A．35° B．45° C．55° D．65°
组卷：338引用：4难度：0.8
解析
6．如图是天安门周围的景点分布示意图．在图中，分别以正东，正北方向为x轴，y轴的正方向建立平面直角坐标系．如果表示景山的点的坐标为（0，4），表示王府井的点的坐标为（3，1），则表示人民大会堂的点的坐标为（　　）
A．（3，2） B．（-1，2） C．（-1，-1） D．（-1，-2）
组卷：229引用：5难度：0.6
解析

7．下列命题中，假命题是（　　）

A．对顶角相等

B．同一平面内，过一点有且只有一条直线与已知直线垂直

C．两条直线被第三条直线所截，同旁内角互补

D．若一个角的两边分别与另一个角的两边平行，那么这两个角相等或互补

组卷：179引用：1难度：0.5

解析

8．如图，四边形ABCD中，AC，BD交于点O，如果∠BAC=∠DCA，那么以下四个结论中错误的是（　　）
A．AD∥BC B．AB∥CD
C．∠ABD=∠CDB D．∠BAD+∠ADC=180°
组卷：540引用：6难度：0.8
解析
9．我国古代数学著作《九章算术》“盈不足”一章中记载：“今有大器五、小器一容三斛；大器一、小器五容二斛，问大小器各容几何？”意思是：今有大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛．问1个大容器、1个小容器的容量各是多少斛？设1个大容器的容量为x斛，1个小容器的容量为y斛，则下列方程组正确的是（　　）
A．
5
x
+
y
=
3
x
+
5
y
=
2
B．
5
x
+
y
=
2
x
+
5
y
=
3
C．
5
x
+
3
y
=
1
x
+
2
y
=
5
D．
3
x
+
y
=
5
2
x
+
5
y
=
1
组卷：550引用：11难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共46分，19题3分，20题4分，每题5分，每题6分）

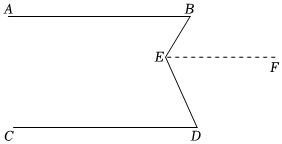26．阅读下面材料：
彤彤遇到这样一个问题：
已知：如图，AB∥CD，E为AB，CD之间一点，连接BE，DE，得到∠BED．
求证：∠BED=∠B+∠D．
彤彤是这样做的：
过点E作EF∥AB，
则有∠BEF=∠B．
∵AB∥CD，
∴EF∥CD．
∴∠FED=∠D
∴∠BEF+∠FED=∠B+∠D．
即∠BED=∠B+∠D．
请你参考彤彤思考问题的方法，解决问题：如图，
已知：直线 a∥b,点A，B在直线a上，点C，D在直线b上，连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．
（1）如图1，当点B在点A的左侧时，若∠ABC=60°，∠ADC=70°，则∠BED的度数为
；
（2）如图2，当点B在点A的右侧时，请你猜想并证明∠ABC、∠ADC 与∠BED 之间的数量关系．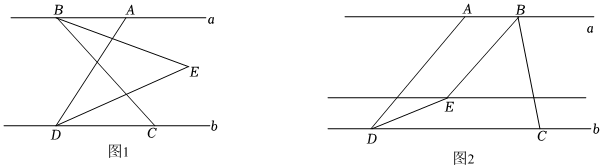

组卷：360引用：1难度：0.5
解析
27．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“邻近距离”，记为d（图形M，图形N）．
已知点A（-2，-2），B（3，-2），C（3，3），D（-2，3）．
（1）d（点O，线段AB）=
；
（2）若点G在x轴上，且d（点G，线段AB）＞2，求点G的横坐标a的取值范围；
（3）依次连接A，B，C，D四点，得到正方形ABCD（不含图形内部），记为图形M，点E（t,0），点F（0，
3
2
-t）均不与点O重合，线段EO，OF组成的图形记为图形N，若d（图形M，图形N）=1，直接写出t的值．

组卷：358引用：2难度：0.6
解析