2022-2023学年云南师大附中高三（上）第六次月考数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知集合A={x|-2＜x＜2}，

  B

  =

  {

  x

  |

  x

  -

  3

  x

  -

  1

  ≤

  0

  }

  ，则A∩B=（　　）

  A．{x|1≤x≤2}

  B．{x|1＜x＜2}

  C．{x|-2＜x≤3}

  D．{x|-2≤x＜3}
  组卷：239引用：6难度：0.7

  解析

• 2．若（1+i）²z=1-i,则z在复平面内对应的点所在象限为（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：5引用：3难度：0.7

  解析

• 3．窗花是贴在窗纸或窗户玻璃上的剪纸，是中国古老的汉族传统民间艺术之一，它历史㤵久，风格独特，深受国内外人士所喜爱．如图甲是一个正八边形窗花隔断，图乙是从窗花图中抽象出的几何图形示意图．已知正八边形ABCDEFGH的边长为

  2

  2

  ，M是正八边形ABC-DEFGH边上任意一点，则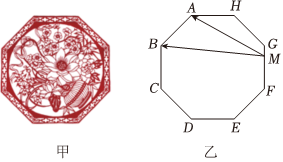

  MA

  •

  MB

  的最大值为（　　）
  

  A． 30 + 4 2

  B． 28 + 8 2

  C． 26 + 16 2

  D． 24 + 16 2
  组卷：122引用：4难度：0.6

  解析

• 4．数字1，2，3，4，5任意组成没有重复数字的四位数，则它是奇数的概率是（　　）

  A． 1 5

  B． 2 5

  C． 3 5

  D． 4 5
  组卷：12引用：4难度：0.8

  解析

• 5．函数

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  -

  xsinx

  的图象大致为（　　）

  A．	B．
  C．	D．
  组卷：175引用：5难度：0.7

  解析

• 6．血氧饱和度是血液中被氧结合的氧合血红蛋白的容量占全部可结合的血红蛋白容量的百分比，即血液中血氧的浓度，它是呼吸循环的重要生理参数．正常人体的血氧饱和度一般不低于95%，在95%以下为供氧不足．在环境模拟实验室的某段时间内，可以用指数模型：

  S

  （

  t

  ）

  =

  S

  0

  e

  K

  t

  描述血氧饱和度S（t）（单位：%）随给氧时间t（单位：时）的变化规律，其中S₀为初始血氧饱和度，K为参数．已知S₀=60，给氧1小时后，血氧饱和度为70．若使得血氧饱和度达到正常值，则给氧时间至少还需要（取ln6=1.79，ln7=1.95，ln12=2.48，ln19=2.94）（　　）

  A．1.525小时

  B．1.675小时

  C．1.725小时

  D．1.875小时
  组卷：154引用：7难度：0.7

  解析

• 7．球面几何中，球面两点之间最短的距离为经过这两点的大圆的劣弧长，称为测地线．已知A，B，C是球O球面上的三个点，AC⊥BC，AC=BC=1，三棱锥O-ABC的体积为

  2

  12

  ，则A，B两点测地线长为（　　）

  A．2

  B．4

  C． π 2

  D． π 4
  组卷：18引用：4难度：0.5

  解析

四、解答题（共70分.解答应写出文字说明，证明过程或演算步骤）

• 21．已知点

  M

  （

  3

  ，

  2

  ）

  在双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  上，C的左焦点为F，点F到C的渐近线的距离为1，过点F的直线l与C的左支交于A，B两点．
  （1）求C的方程；
  （2）作MN垂直于x轴于点N，若△ABN的外接圆圆心P在y轴上，求l的方程．
  组卷：4引用：3难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  1

  +

  lnx

  ax

  ，a＞0．
  （1）若f（x）≤1，求a的取值范围；
  （2）证明：若存在x₁，x₂，使得f（x₁）=f（x₂），则

  x

  2

  1

  +

  x

  2

  2

  ＞

  2

  ．
  组卷：26引用：3难度：0.6

  解析