2022-2023学年浙江省金华市义乌市稠州中学九年级（上）开学数学试卷

一、单选题（每小题3分，共30分）

• 1．下列方程中，属于一元二次方程的是（　　）

  A．2x+y=3

  B．x2+3x=0

  C． 1 x 2 - x = 0

  D．2x+1=0
  组卷：619引用：4难度：0.8

  解析

• 2．下列计算正确的是（　　）

  A． 27 ÷ 3 =3

  B． 2 + 5 = 7

  C． 8 = 4 2

  D． （ - 3 ） 2 =-3
  组卷：180引用：7难度：0.7

  解析

• 3．一个多边形的内角和与外角和相等，则这个多边形的边数为（　　）

  A．8

  B．6

  C．5

  D．4
  组卷：495引用：5难度：0.8

  解析

• 4．下列图形中既是中心对称图形，又是轴对称图形是（　　）
  

  A．圆	B．平行四边形
  C．等边三角形	D．等腰直角三角形
  组卷：226引用：4难度：0.8

  解析

• 5．一元二次方程

  y

  2

  +

  y

  -

  3

  4

  =

  0

  ，配方后可化为（　　）

  A． （ y + 1 2 ） 2 = 1

  B． （ y - 1 2 ） 2 = 1

  C． （ y + 1 2 ） 2 = 3 4

  D． （ y - 1 2 ） 2 = 3 4
  组卷：36引用：3难度：0.7

  解析

• 6．假设命题“

  a

  2

  =a”不成立，则a与0的大小关系是（　　）

  A．a＜0

  B．a≤0

  C．a≠0

  D．a＞0
  组卷：305引用：5难度：0.6

  解析

• 7．甲、乙两人在相同的条件下，各射靶10次，经过计算：甲、乙射击成绩的平均数都是8环，甲的方差是1.2，乙的方差是2.8．下列说法中正确的是（　　）

  A．甲的众数与乙的众数相同

  B．甲的成绩比乙稳定

  C．乙的成绩比甲稳定

  D．甲的中位数与乙的中位数相同
  组卷：384引用：5难度：0.7

  解析

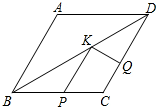• 8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（　　）

  A．1

  B． 3

  C．2

  D． 3 +1
  组卷：2669引用：38难度：0.7

  解析

三、解答题（共8小题，66分）

• 23．已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P、G不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连接EF．
  （1）如图1，当点P与点G分别在线段BC与线段AD上时．
  ①求证：DG=2PC；
  ②求证：四边形PEFD是菱形；
  （2）如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．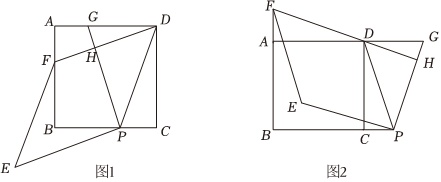
  
  组卷：1693引用：8难度：0.1

  解析

• 24．在平面直角坐标系中，O为原点，△OAB是等腰直角三角形，∠OBA=90°，BO=BA，顶点A（4，0），点B在第一象限，矩形OCDE的顶点E（-

  7

  2

  ，0），点C在y轴的正半轴上，点D在第二象限，射线DC经过点B．
  （Ⅰ）如图①，求点B的坐标；
  （Ⅱ）将矩形OCDE沿x轴向右平移，得到矩形O′C′D′E′，点O，C，D，E的对应点分别为O′，C′，D′，E′．设OO′=t,矩形O′C′D′E′与△OAB重叠部分的面积为S．
  ①如图②，当点E′在x轴正半轴上，且矩形O′C′D′E′与△OAB重叠部分为四边形时，D′E′与OB相交于点F，试用含有t的式子表示S，并直接写出t的取值范围；
  ②当

  5

  2

  ≤t≤

  9

  2

  时，求S的取值范围（直接写出结果即可）．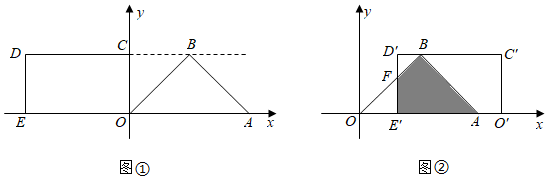
  组卷：3549引用：5难度：0.5

  解析