2022-2023学年河南省驻马店市驿城区七年级（下）期末数学试卷

一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的.

• 1．下列图形不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：61引用：5难度：0.9

  解析

• 2．随着微电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.00000065mm²，将0.00000065用科学记数法表示为（　　）

  A．6.5×10-6

  B．6.5×10-7

  C．65×10-8

  D．0.65×10-7
  组卷：717引用：17难度：0.9

  解析

• 3．下列计算正确的是（　　）

  A．a3•a4=a12	B．（-3ab3）2=-6ab6
  C．（a-3）2=a2-9	D．（-x+y）（x+y）=y2-x2
  组卷：24引用：2难度：0.7

  解析

• 4．若三角形的两边长分别为4cm和9cm,则下列长度的线段能作为第三边的是（　　）

  A．4cm

  B．9cm

  C．13cm

  D．14cm
  组卷：53引用：1难度：0.5

  解析

• 5．如图，直线AB∥CD，直线EF分别与直线AB、CD交于点E、F，点G在直线CD上，EF⊥EG．若∠1=50°，则∠2的度数是（　　）

  A．140°

  B．130°

  C．120°

  D．110°
  组卷：165引用：2难度：0.7

  解析

• 6．如图，点B、E、C、F在一条直线上，已知AB∥DF，AB=DF，下列条件中，不能判断△ABC≌△DEF的是（　　）

  A．BE=CF

  B．AC=DE

  C．∠A=∠D

  D．AC∥DE
  组卷：143引用：1难度：0.5

  解析

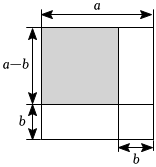• 7．如图，边长为a的大正方形中有一个边长为b的小正方形，小颖将阴影部分的面积用两种不同的方法表示，能验证的等式是（　　）

  A．（a-b）2=a2-2ab+b2	B．（a+b）2=a2+2ab+b2
  C．（a+b）（a-b）=a2-b2	D．b（a-b）=ab-b2
  组卷：101引用：2难度：0.7

  解析

三、解答题（本大题共8个小题，共75分）

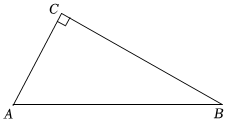• 22．如图，在△ABC中，∠ACB=90°，AC＜BC．
  （1）尺规作图：①在线段BC上求作一点P，使PA=PB；②连接AP，以点A为圆心，AP的长为半径画弧，交BC的延长线于点Q，连接AQ．（保留作图痕迹，不写作法）
  （2）在（1）的条件下，若∠B=25°，求∠PAC的度数；
  （3）在（1）的条件下，若BC=8，求△APQ的周长．
  组卷：71引用：3难度：0.5

  解析

• 23．【自主探究】（1）如图1，在四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，且∠EAF=45°，若∠B=∠ADF=90°，BE=3，DF=5，请计算线段EF的长度．
  小明同学的做法是延长CD至点G，使得DG=BE，连接AG，他发现根据条件可证明△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，又和同学讨论发现，利用SAS可证明△AEF≌△AGF，就能解决问题．那么他的结论是：线段EF的长度为

  ；
  【灵活运用】（2）如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，且∠EAF=45°，若∠B和∠ADF都不是直角，但满足∠B+∠ADF=180°，请猜想线段BE、EF、DF之间的数量关系：

  ；
  【拓展延伸】（3）如图3，在四边形ABCD中，AB=AD，∠BAD=120°，点E、F分别在边BC、CD上，且∠EAF=60°，∠B+∠ADF=180°，请问（2）中线段BE、EF、DF之间的数量关系是否仍然成立，并说明理由．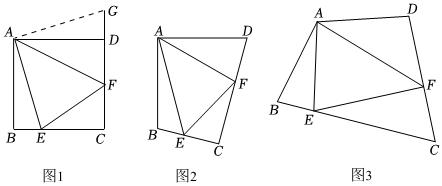
  
  组卷：142引用：1难度：0.4

  解析