2023-2024学年浙江省杭州外国语国语学校九年级(上)月考数学试卷(10月份)
发布:2024/9/14 12:0:8
一.选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中只有一项是符合要求的,请将正确答案填在答题卷的相应位置上)
-
1.华为Mate20系列搭载了麒麟980芯片,这个被华为称之为全球首个7纳米工艺的AI芯片,拥有8个全球第一,7纳米就是0.000 000 007米.数据0.000 000 007用科学记数法表示为( )
组卷:2588引用:20难度:0.9 -
2.已知
,则a4=b3的值是( )a-bb组卷:2523引用:23难度:0.7 -
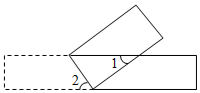 3.将一个长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )组卷:478引用:5难度:0.8
3.将一个长方形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )组卷:478引用:5难度:0.8 -
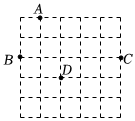 4.如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )组卷:434引用:7难度:0.7
4.如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )组卷:434引用:7难度:0.7 -
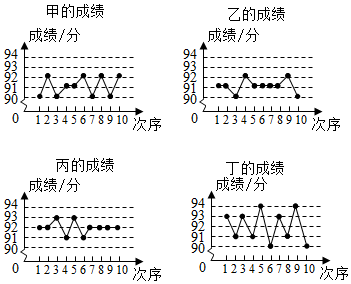 5.甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )组卷:630引用:7难度:0.7
5.甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )组卷:630引用:7难度:0.7 -
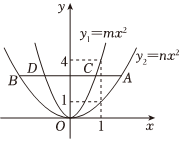 6.如图,直线x=1与抛物线和抛物线y1=mx2分别交于点(1,4)、(1,1),直线AB∥x轴,与抛物线y2=nx2交于C、D两点,与抛物线y1=mx2交于A、B两点,则y2=nx2=( )ABCD
6.如图,直线x=1与抛物线和抛物线y1=mx2分别交于点(1,4)、(1,1),直线AB∥x轴,与抛物线y2=nx2交于C、D两点,与抛物线y1=mx2交于A、B两点,则y2=nx2=( )ABCD
组卷:216引用:3难度:0.5 -
7.有理数a、b、x、y同时满足以下关系式:x+y=a+b,y-x<a-b,b>a,则a、b、x、y的大小关系为( )
组卷:368引用:2难度:0.7 -
8.已知25a•52b=56,4b÷4c=4,则代数式a2+ab+3c值是( )
组卷:3945引用:10难度:0.5
三、解答题(本题有8小题,共72分.解答应写出文字说明、证明过程或推演步骤)
-
23.综合与实践
(1)【操作发现】如图1,诸葛小组将正方形纸片ABCD沿过点A的直线折叠,使点B落在正方形内部的点M处,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,请写出图中的一个45°角;
(2)【拓展探究】如图2,孔明小组继续将正方形纸片沿EF继续折叠,点C的对应点恰好落在折痕AE上的点N处,连接NF交AM于点P.
①∠AEF=度;②若,求线段PM的长;AB=3
(3)【迁移应用】如图3,在矩形ABCD中,点E,F分别在边BC,CD上,将矩形ABCD沿AE,AF折叠,点B落在点M处,点D落在点G处,点A,M,G恰好在同一直线上,若点F为CD的三等分点,AB=3,AD=5,请直接写出线段BE的长.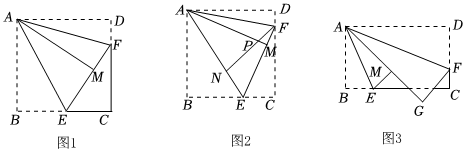 组卷:1012引用:4难度:0.1
组卷:1012引用:4难度:0.1 -
24.如图,抛物线y=ax2+bx-1(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,抛物线的对称轴交x轴于点D(3,0),过点B作直线l⊥x轴,过点D作DE⊥CD,交直线l于点E.
(1)求抛物线的解析式;
(2)如图,点P为第三象限内抛物线上的点,连接CE和BP交于点Q,当时,求点P的坐标;BQPQ=57
(3)在x轴上是否存在点F,使得∠DEF=45°?若存在,请直接写出点F的坐标;若不存在,请说明理由.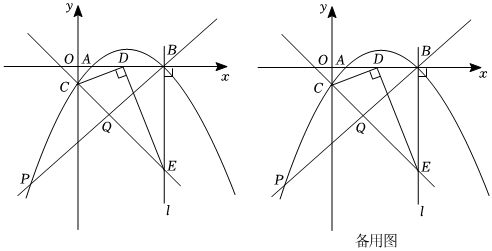 组卷:343引用:2难度:0.1
组卷:343引用:2难度:0.1


