当前位置：试卷中心 > 试卷详情

2023-2024学年福建省厦门市双十中学漳州市校区高三（上）月考数学试卷（10月份）

发布：2024/9/1 18:0:8

1．已知集合A={x|x²-5x-6≤0}，B={x|2^x-1≥1}，则A∩B=（　　）
A．[1，6] B．[1，3] C．[-1，1] D．[2，3]
组卷：13引用：5难度：0.8
解析
2．已知
z
=
1
-
i
1
+
i
，其中i为虚数单位，则
z
+
|
z
|
=（　　）
A．1+i B．1-i C．2i D．2
组卷：26引用：3难度：0.8
解析
3．已知
|
a
|
=
2
|
b
|
，若
a
与
b
的夹角为120°，则
2
b
-
a
在
a
上的投影向量为（　　）
A．
3
-
3
a
B．
-
3
2
a
C．
-
1
2
a
D．
3
a
组卷：490引用：10难度：0.8
解析
4．已知α，β都为锐角，
cosα
=
1
7
，
cos
（
α
+
β
）
=
-
11
14
，则cosβ等于（　　）
A．
1
2
B．-
71
98
C．-
1
2
D．
71
98
组卷：441引用：8难度：0.8
解析
5．已知数列{a_n}为各项为正数的等比数列，且a₁，a₃，a₂成等差数列，则数列{a_n}（　　）
A．单调递增 B．单调递减
C．先递增后递减 D．是常数列
组卷：53引用：5难度：0.7
解析
6．已知a＞b＞1，则以下四个数中最大的是（　　）
A．log_ba B．log_2b2a C．log_3b3a D．log_4b4a
组卷：1015引用：7难度：0.6
解析
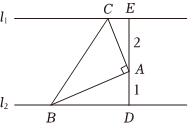7．如图，已知直线l₁∥l₂，A为l₁，l₂之间一定点，并且点A到l₁的距离为2，到l₂的距离为1，B为直线l₂上一动点，作AC⊥AB，且使AC与直线l₁交于点C，则△ABC面积的最小值为（　　）
A．1 B．
3
2
C．2 D．4
组卷：532引用：4难度：0.5
解析

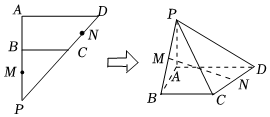21．如图，在等腰直角三角形PAD中，∠A=90°，AD=8，AB=3，B，C分别是PA，PD上的点，且AD∥BC，M，N分别为BP，CD的中点，现将△BCP沿BC折起，得到四棱锥P-ABCD，连结MN．
（1）证明：MN∥平面PAD；
（2）在翻折的过程中，当PA=4时，求平面PBC与平面PCD夹角的余弦值．
组卷：116引用：5难度：0.5
解析
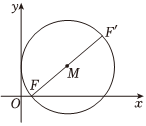22．如图，已知动圆M过定点F（1，0）且与y轴相切，点F关于圆心M的对称点为F′，点F′的轨迹为H．
（1）求曲线H的方程；
（2）一条直线AB经过点F，且交曲线H于A、B两点，点C为直线x=-1上的动点．
①求证：∠ACB不可能是钝角；
②是否存在这样的点C，使得△ABC是正三角形？若存在，求点C的坐标；否则，说明理由．
组卷：200引用：11难度：0.5
解析