2023-2024学年云南省昆明市官渡二中高三（上）期初数学试卷

一、选择题；本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．设集合A={x|-1≤x＜1}，Z为整数集，则A∩Z=（　　）

  A．{-1，0}

  B．{-1，1}

  C．{0，1}

  D．{-1，0，1}
  组卷：37引用：3难度：0.9

  解析

• 2．在复平面内，复数z对应的点为（-1，2），则

  z

  -

  i

  1

  +

  i

  =（　　）

  A．1

  B．i

  C．-i

  D． - 3 2 - 5 2 i
  组卷：40引用：5难度：0.8

  解析

• 3．已知方程（x²-mx+27）（x²-nx+27）=0的四个根组成以1为首项的等比数列，则|m-n|=（　　）

  A．8

  B．12

  C．16

  D．20
  组卷：282引用：5难度：0.7

  解析

• 4．若

  sinθ

  =

  5

  cosθ

  ，则tan2θ=（　　）

  A．- 5 3

  B． 5 3

  C．- 5 2

  D． 5 2
  组卷：1022引用：6难度：0.7

  解析

• 5．已知椭圆E：

  x

  2

  11

  +

  y

  2

  2

  =

  1

  与双曲线C：

  x

  2

  a

  2

  -

  y

  2

  5

  =

  1

  （a＞0，b＞0）有相同的焦点，则双曲线C的渐近线方程为（　　）

  A． y =± 3 5 5 x

  B． y =± 5 3 x

  C． y =± 2 5 5 x

  D． y =± 5 2 x
  组卷：180引用：9难度：0.7

  解析

• 6．已知f（x）是定义在R上的偶函数，其图象关于点（1，0）对称．以下关于f（x）的结论：
  ①f（x）是周期函数；
  ②f（x）满足f（x）=f（4-x）；
  ③f（x）在（0，2）单调递减；
  ④f（x）=cos

  πx

  2

  是满足条件的一个函数，
  其中正确结论的个数是（　　）

  A．4

  B．3

  C．2

  D．1
  组卷：67引用：2难度：0.6

  解析

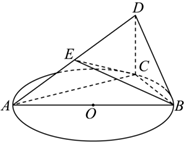• 7．如图，△ABC内接于圆O，AB为圆O的直径，AB=5，BC=3，CD⊥平面ABC，E为AD的中点，且异面直线BE与AC所成角为60°，则点A到平面BCE的距离为（　　）

  A． 8 21 3

  B． 8 7 7

  C． 4 21 7

  D． 4 7 3
  组卷：135引用：3难度：0.5

  解析

四、解答题；本题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤．

• 21．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  5

  5

  ，短轴长为4．
  （1）求C的标准方程；
  （2）过C的左焦点F作相互垂直的两条直线l₁，l₂（均不垂直于x轴），l₁交C于A，B两点，l₂交C于C，D两点．设线段AB，CD的中点分别为P，Q，证明：直线PQ恒过x轴上一定点．
  组卷：13引用：2难度：0.5

  解析

• 22．已知函数f（x）=1-x-axlnx（a∈R），g（x）=

  f

  （

  x

  ）

  x

  +

  1

  ．
  （1）当a=-

  1

  2

  时，求f（x）的最小值；
  （2）当0＜a≤1时，g（x）≤m恒成立，求整数m的最小值．
  组卷：135引用：2难度：0.6

  解析