2023-2024学年江西省宜春八中九年级（上）第一次段考数学试卷

一、单项选择题（本大题共6小题，每小题3分，共18分）

• 1．抛物线y=（x-2）²+1的顶点坐标是（　　）

  A．（-2，-1）

  B．（-2，1）

  C．（2，-1）

  D．（2，1）
  组卷：1256引用：65难度：0.9

  解析

• 2．下列方程中，是关于x的一元二次方程的是（　　）

  A． 2 x +x=3	B．x2+2x-3=0
  C．4x+3=x	D．x2+x+1=x2-2x
  组卷：1466引用：10难度：0.8

  解析

• 3．用配方法解一元二次方程x²-4x-2=0的过程中，配方正确的是（　　）

  A．（x+2）2=2

  B．（x-2）2=2

  C．（x+2）2=6

  D．（x-2）2=6
  组卷：321引用：6难度：0.7

  解析

• 4．将抛物线y=-x²+2x+1向下平移两个单位，以下说法错误的是（　　）

  A．开口方向不变	B．对称轴不变
  C．y随x的变化情况不变	D．与y轴的交点不变
  组卷：70引用：2难度：0.5

  解析

• 5．已知m,n是一元二次方程x²+3x-2023=0的两个实数根，则代数式m²+4m+n的值等于（　　）

  A．2020

  B．2021

  C．2022

  D．2023
  组卷：216引用：2难度：0.5

  解析

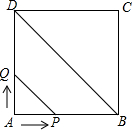• 6．如图，正方形ABCD的边长为4cm,动点P、Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动，设运动时间为x（单位：s），四边形PBDQ的面积为y（单位：cm²），则y与x（0≤x≤8）之间函数关系可以用图象表示为（　　）

  A．

  B．

  C．

  D．
  组卷：1652引用：51难度：0.7

  解析

二、填空题（本大题共6小题，每小题3分，共18分）

• 7．已知x²=9，则x=

  ．
  组卷：676引用：3难度：0.8

  解析

五、解答题（本大题共2个小题，每小题9分，共18分）

• 22．课本再现：
  思考
  我们知道，两组对边分别平行或相等的四边形是平行四边形．如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢？
  

  通过证明我们又得到了平行四边形的一个判定定理：一组对边平行且相等的四边形是平行四边形．

  
  （1）定理证明：为了证明该定理，小明同学画出了图形，如图1，并写出了“已知”和“求证”，请你完成证明过程．已知：在四边形ABCD中，AB∥CD，AB=CD，求证：四边形ABCD是平行四边形．
  （2）定理应用：如图2，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE=CF，作EG∥FH，分别与对角线BD交于点G、H，连接EH、FG．
  ①求证：四边形EHFG是平行四边形；
  ②连接DF，若BF=DF，EG=3，求四边形EGFH的周长．
  组卷：115引用：2难度：0.4

  解析

六、解答题（本大题12分）

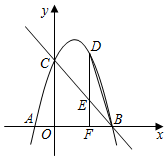• 23．如图，已知抛物线y=ax²+bx+5与x轴交于A（-1，0），B（5，0）两点（点A在点B的左侧），与y轴交于点C．
  （1）求抛物线的解析式；
  （2）点D是第一象限内抛物线上的一个动点（与点C，B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD，直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．
  （3）若M为抛物线对称轴上一动点，使得△MBC为直角三角形，请直接写出点M的坐标．
  组卷：4778引用：25难度：0.1

  解析