2022-2023学年广东省江门市新会区尚雅中学八年级（上）期中数学试卷

一、选择题（每小题3分，共30分）

• 1．下列图形中，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：330引用：6难度：0.7

  解析

• 2．下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（　　）

  A．2，2，4

  B．3，2，6

  C．1，2，2

  D．1，2，3
  组卷：175引用：5难度：0.7

  解析

• 3．若点A（x,1）与B（-2，y）关于x轴对称，则（　　）

  A．x=-2，y=1

  B．x=-2，y=-1

  C．x=2，y=-1

  D．x=2，y=1
  组卷：369引用：6难度：0.9

  解析

• 4．下列运算正确的是（　　）

  A．（x3）2=x5	B．（-x）5=-x5
  C．x3•x2=x6	D．3x2+2x3=5x5
  组卷：2039引用：15难度：0.9

  解析

• 5．一个凸多边形的内角和与外角和之比为2：1，则这个多边形的边数为（　　）

  A．5

  B．6

  C．7

  D．8
  组卷：641引用：13难度：0.6

  解析

• 6．若mx+6y与x-3y的乘积中不含有xy项，则m的值为（　　）

  A．0

  B．2

  C．3

  D．6
  组卷：904引用：3难度：0.7

  解析

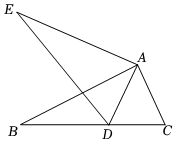• 7．如图，△ABC≌△AED，点D在BC边上．若∠EAB=50°，则∠ADE的度数是（　　）

  A．50°

  B．60°

  C．65°

  D．30°
  组卷：835引用：8难度：0.7

  解析

• 8．如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（　　）

  A．90°- 1 2 α

  B．90°+ 1 2 α

  C． 1 2 α

  D．360°-α
  组卷：16507引用：116难度：0.7

  解析

• 9．如图，点E在等边△ABC的边BC上，BE=4，射线CD⊥BC，垂足为点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+FP的值最小时，BF=5，则AB的长为（　　）

  A．7

  B．8

  C．9

  D．10
  组卷：1871引用：7难度：0.6

  解析

五、解答题（三）（每小题10分，共20分）

• 26．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，以AB为一边向上作等边三角形ABD，点E在BC垂直平分线上，且EB⊥AB，连接CE、AE、CD．
  （1）判断△CBE的形状，并说明理由；
  （2）求证：AE=DC；
  （3）若AE，CD相交于点F，AB，CD相交于点G，求∠AFD的度数．
  组卷：73引用：3难度：0.5

  解析

六、解答题（四）（每小题12分。共13分）

• 27．如图，△ABC和△AOD是等腰直角三角形，AB=AC，AO=AD，∠BAC=∠OAD=90°，点O是△ABC内的一点，∠BOC=130°．
  （1）求证：OB=DC；
  （2）求∠DCO的大小；
  （3）设∠AOB=α，那么当α为多少度时，△COD是等腰三角形．
  组卷：1199引用：17难度：0.1

  解析