2023年广东省茂名一中高考数学三模试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．集合A={y|y=2^x}，B={x|y=log₂（3x-2）}，则（∁_RB）∩A=（　　）

  A． （ 2 3 ， + ∞ ）

  B． [ 0 ， 2 3 ]

  C． （ 0 ， 2 3 ]

  D． （ - ∞ ， 2 3 ]
  组卷：239引用：4难度：0.8

  解析

• 2．复数

  1

  i

  -

  2

  的虚部为（　　）

  A． 1 5

  B． 1 5 i

  C． - 1 5

  D． - 1 5 i
  组卷：169引用：4难度：0.9

  解析

• 3．给出下列四个命题，其中正确命题为（　　）

  A．“∀x＞0，x2+x＞1”的否定是“∃x0＞0， x 2 0 +x0＜1”

  B．“α＞β”是“sinα＞sinβ”的必要不充分条件

  C．∃α，β∈R，使得sin（α+β）=sinα+sinβ

  D．“a＞b”是“2a＞2b”的充分不必要条件
  组卷：167引用：3难度：0.6

  解析

• 4．定义：将24小时内降水在平地上积水厚度（mm）来判断降雨程度；其中小雨（0mm-10mm），中雨（10mm-25mm），大雨（25mm-50mm），暴雨（50mm-100mm）；小明用一个圆锥形容器接了24小时的雨水，则这天降雨属于哪个等级（　　）

  A．小雨

  B．中雨

  C．大雨

  D．暴雨
  组卷：557引用：12难度：0.7

  解析

• 5．已知a,b为正实数，直线y=x-2a与曲线y=ln（x+b）相切，则

  1

  a

  +

  2

  b

  的最小值是（　　）

  A．8

  B． 4 2

  C．6

  D． 2 2
  组卷：477引用：9难度：0.5

  解析

• 6．由数字0，1，2，3，4组成的各位上没有重复数字的五位数中，从小到大排列第88个数为（　　）

  A．42031

  B．42103

  C．42130

  D．42301
  组卷：411引用：4难度：0.5

  解析

• 7．斐波那契数列{a_n}满足a₁=a₂=1，a_n=a_n-1+a_n-2（n≥3），其每一项称为“斐波那契数”．如图，在以斐波那契数为边长的正方形拼成的长方形中，利用下列各图中的面积关系，推出

  a

  2

  1

  +

  a

  2

  2

  +

  …

  +

  a

  2

  2023

  a

  2023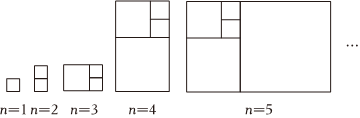

  是斐波那契数列的第（　　）项．
  

  A．2022

  B．2023

  C．2024

  D．2025
  组卷：202引用：4难度：0.5

  解析

四、解答题：本题共6小题，共70分.

• 21．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的离心率为2．
  （1）求双曲线C的渐近线方程；
  （2）若双曲线C的右焦点为F，若直线EF与C的左，右两支分别交于E，D两点，过E作l：x=

  a

  2

  的垂线，垂足为R，试判断直线DR是否过定点，若是，求出定点的坐标；若不是，请说明理由．
  组卷：108引用：3难度：0.6

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  ax

  +

  （

  a

  -

  1

  ）

  lnx

  +

  1

  x

  ，a∈R．
  （1）讨论函数f（x）的单调性；
  （2）若关于x的方程

  f

  （

  x

  ）

  =

  x

  e

  x

  -

  lnx

  +

  1

  x

  有两个不相等的实数根x₁，x₂，
  （ⅰ）求实数a的取值范围；
  （ⅱ）求证：

  e

  x

  1

  x

  2

  +

  e

  x

  2

  x

  1

  ＞

  2

  a

  x

  1

  x

  2

  ．
  组卷：393引用：8难度：0.3

  解析