2023年江苏省淮安市清江浦区开明中学中考数学模拟试卷(一)
发布:2024/5/16 8:0:9
一、选择题(每小题3分,共24分)
-
1.下列四个数中,最小的一个数是( )
组卷:23引用:4难度:0.8 -
2.计算(x4)3=( )
组卷:56引用:3难度:0.7 -
3.下列几何体的左视图和俯视图相同的是( )
组卷:744引用:16难度:0.8 -
4.数据14、15、16、16、16、18的众数为( )
组卷:58引用:6难度:0.7 -
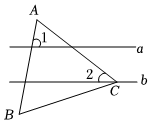 5.如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的度数为( )组卷:1429引用:16难度:0.7
5.如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的度数为( )组卷:1429引用:16难度:0.7 -
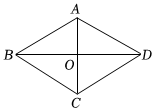 6.如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的面积是( )组卷:607引用:6难度:0.5
6.如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的面积是( )组卷:607引用:6难度:0.5 -
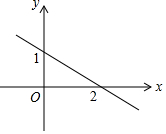 7.一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )组卷:2205引用:16难度:0.7
7.一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )组卷:2205引用:16难度:0.7 -
8.若关于x的方程x2-x-m=0没有实数根,则m的值可以为( )
组卷:2127引用:30难度:0.8
二、填空题(每小题3分,共24分)
-
9.分解因式:x2-xy=.
组卷:1117引用:48难度:0.9
三、解答题(共11小题,102分)
-
26.我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
(1)【方法回顾】
证明:三角形中位线定理.
已知:如图,在△ABC中,D、E分别是AB、AC的中点.
求证:DE∥BC,.DE=12BC
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成,下面是其中一种证法的添加辅助线方法,阅读并完成填空:
添加辅助线,如图1,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.可证△ADE≌,根据全等三角形对应边相等可得DE=EF,然后判断出四边形BCFD是 ,根据图形性质可证得DE∥BC,.DE=12BC
(2)【方法迁移】
如图2,在四边形ABCD中,AD∥BC,∠A=90°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若,DF=4,∠GEF=90°,求GF的长.AG=3
(3)【定理应用】
如图3,在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,,延长BC至点E,使DE=DG,延长ED交AB于点F,直接写出CGBG=K(K>1)的值(用含K的式子表示).ABAF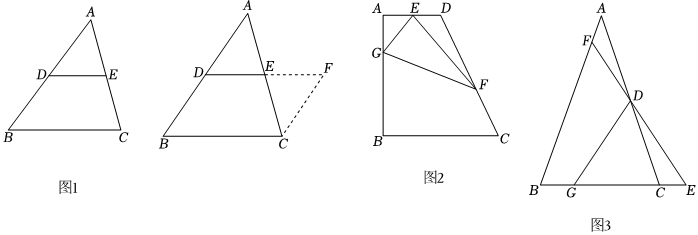 组卷:588引用:3难度:0.3
组卷:588引用:3难度:0.3 -
27.如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+3(a<0)与x轴分别交于点A(-3,0)和点B(1,0),与y轴交于点C,P为抛物线上一动点.
(1)写出抛物线的对称轴为直线 ,抛物线的解析式为 ;
(2)如图2,连结AC,若P在AC上方,作PQ∥y轴交AC于Q,把上述抛物线沿射线PQ的方向向下平移,平移的距离为h(h>0),在平移过程中,该抛物线与直线AC始终有交点,求h的最大值;
(3)若P在AC上方,设直线AP,BP与抛物线的对称轴分别相交于点F,E,请探索以A,F,B,G(G是点E关于x轴的对称点)为顶点的四边形面积是否随着P点的运动而发生变化,若不变,求出这个四边形的面积;若变化,说明理由.
(4)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P的横坐标;若不存在,请说明理由.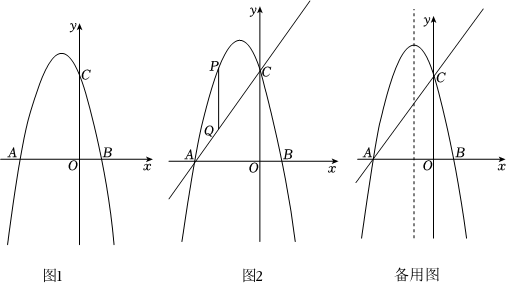 组卷:258引用:5难度:0.3
组卷:258引用:5难度:0.3


